Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 3 trang 103 và 104 sách giáo khoa Toán 9 tập 1 chương trình Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
Trong Hình 25, cột thẳng đứng và biển quảng cáo có dạng hình tròn gợi nên hình ảnh của đường thẳng và đường tròn không giao nhau. Theo em, đường thẳng và đường tròn không giao nhau thì chúng có điểm chung hay không?
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 104SGK Toán 9 Cánh diều
Cho điểm \(O\) và đường thẳng \(a\) thỏa mãn khoảng cách từ \(O\) đến đường thẳng \(a\) bằng 4cm. Xác định vị trí tương đối của đường thẳng \(a\) và các đường tròn \(\left( {O;3cm} \right),\left( {O;4cm} \right),\left( {O;5cm} \right)\).
Phương pháp giải:
Dựa vào hệ thức giữa \(d\) và \(R\) để xác định.
Lời giải chi tiết:
Khoảng cách từ \(O\) đến đường thẳng \(a\) bằng 4cm \( \Rightarrow d = 4\left( {cm} \right)\).
+ Với đường tròn \(\left( {O;3cm} \right)\) ta có: \(4 > 3 \Rightarrow d > R\).
Vậy đường thẳng \(a\) và đường tròn \(\left( {O;3cm} \right)\) không giao nhau.
+ Với đường tròn \(\left( {O;4cm} \right)\) ta có: \(4 = 4 \Rightarrow d = R\).
Vậy đường thẳng \(a\) và đường tròn \(\left( {O;4cm} \right)\) tiếp xúc nhau.
+ Với đường tròn \(\left( {O;5cm} \right)\) ta có: \(4 < 5 \Rightarrow d < R\).
Vậy đường thẳng \(a\) và đường tròn \(\left( {O;5cm} \right)\) cắt nhau.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 103 SGK Toán 9 Cánh diều
Quan sát Hình 26.
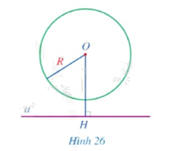
a) Cho biết đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) có bao nhiêu điểm chung.
b) So sánh độ dài đoạn thẳng \(OH\) và \(R\).
Phương pháp giải:
Dựa vào quan sát trực quan để đưa ra nhận xét.
Lời giải chi tiết:
a) Đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) không có điểm chung.
b) \(OH > R\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 103 SGK Toán 9 Cánh diều
Trong Hình 25, cột thẳng đứng và biển quảng cáo có dạng hình tròn gợi nên hình ảnh của đường thẳng và đường tròn không giao nhau. Theo em, đường thẳng và đường tròn không giao nhau thì chúng có điểm chung hay không?

Phương pháp giải:
Dựa vào quan sát trực quan để đưa ra nhận xét.
Lời giải chi tiết:
Đường thẳng và đường tròn không giao nhau không có điểm chung.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 103 SGK Toán 9 Cánh diều
Trong Hình 25, cột thẳng đứng và biển quảng cáo có dạng hình tròn gợi nên hình ảnh của đường thẳng và đường tròn không giao nhau. Theo em, đường thẳng và đường tròn không giao nhau thì chúng có điểm chung hay không?

Phương pháp giải:
Dựa vào quan sát trực quan để đưa ra nhận xét.
Lời giải chi tiết:
Đường thẳng và đường tròn không giao nhau không có điểm chung.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 103 SGK Toán 9 Cánh diều
Quan sát Hình 26.
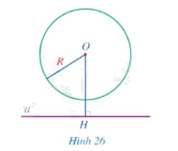
a) Cho biết đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) có bao nhiêu điểm chung.
b) So sánh độ dài đoạn thẳng \(OH\) và \(R\).
Phương pháp giải:
Dựa vào quan sát trực quan để đưa ra nhận xét.
Lời giải chi tiết:
a) Đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) không có điểm chung.
b) \(OH > R\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 104SGK Toán 9 Cánh diều
Cho điểm \(O\) và đường thẳng \(a\) thỏa mãn khoảng cách từ \(O\) đến đường thẳng \(a\) bằng 4cm. Xác định vị trí tương đối của đường thẳng \(a\) và các đường tròn \(\left( {O;3cm} \right),\left( {O;4cm} \right),\left( {O;5cm} \right)\).
Phương pháp giải:
Dựa vào hệ thức giữa \(d\) và \(R\) để xác định.
Lời giải chi tiết:
Khoảng cách từ \(O\) đến đường thẳng \(a\) bằng 4cm \( \Rightarrow d = 4\left( {cm} \right)\).
+ Với đường tròn \(\left( {O;3cm} \right)\) ta có: \(4 > 3 \Rightarrow d > R\).
Vậy đường thẳng \(a\) và đường tròn \(\left( {O;3cm} \right)\) không giao nhau.
+ Với đường tròn \(\left( {O;4cm} \right)\) ta có: \(4 = 4 \Rightarrow d = R\).
Vậy đường thẳng \(a\) và đường tròn \(\left( {O;4cm} \right)\) tiếp xúc nhau.
+ Với đường tròn \(\left( {O;5cm} \right)\) ta có: \(4 < 5 \Rightarrow d < R\).
Vậy đường thẳng \(a\) và đường tròn \(\left( {O;5cm} \right)\) cắt nhau.
Mục 3 trong SGK Toán 9 tập 1 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp liên quan. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết và phân tích cách tiếp cận phù hợp.
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải: (Cung cấp lời giải chi tiết, bao gồm các bước giải, giải thích rõ ràng và sử dụng các công thức liên quan. Ví dụ:)
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải: (Cung cấp lời giải chi tiết tương tự như bài 1)
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải: (Cung cấp lời giải chi tiết tương tự như bài 1)
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải: (Cung cấp lời giải chi tiết tương tự như bài 1)
Để hiểu rõ hơn về cách giải các bài tập trong mục này, chúng ta hãy xem xét một ví dụ minh họa:
(Cung cấp một ví dụ cụ thể và giải chi tiết)
Hy vọng rằng với những lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 3 trang 103, 104 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| a2 - b2 = (a - b)(a + b) | Hiệu hai bình phương |
| (a + b)2 = a2 + 2ab + b2 | Bình phương của một tổng |