Chào mừng các em học sinh đến với lời giải chi tiết bài tập 4 trang 103 SGK Toán 9 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 4 thuộc chương trình học Toán 9 tập 2, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Chúng tôi hy vọng với những hướng dẫn chi tiết này, các em sẽ hiểu rõ hơn về cách tiếp cận và giải quyết các bài toán tương tự.
Chú hề trên sân khấu thường có trang phục như Hình 27a. Mũ của chủ hề có dạng hình nón. Có thể mô phỏng cấu tạo, kích thước chiếc mũ của chú hề như Hình 27b. a) Để phủ kín mặt ngoài chiếc mũ của chú hề như Hình 27b cần bao nhiều centimét vuông giấy màu (không tính phần mép dán và làm tròn kết quả đến hàng đơn vị)? b) Hỏi thể tích phần có dạng hình nón của chiếc mũ chú hề ở Hình 27b bằng bao nhiêu centimét khối (làm tròn kết quả đến hàng phần trăm)?
Đề bài
Chú hề trên sân khấu thường có trang phục như Hình 27a. Mũ của chủ hề có dạng hình nón. Có thể mô phỏng cấu tạo, kích thước chiếc mũ của chú hề như Hình 27b.
a) Để phủ kín mặt ngoài chiếc mũ của chú hề như Hình 27b cần bao nhiều centimét
vuông giấy màu (không tính phần mép dán và làm tròn kết quả đến hàng đơn vị)?
b) Hỏi thể tích phần có dạng hình nón của chiếc mũ chú hề ở Hình 27b bằng bao nhiêu centimét khối (làm tròn kết quả đến hàng phần trăm)?

Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Mặt ngoài là diện tích xung quanh + diện tích phần vành chiếc mũ.
- Sử dụng công thức tính diện tích xung quanh hình nón: \(S_{xq} = \pi rl\)
- Sử dụng công thức tính diện tích hình vành khuyên: \(S = \pi (R^2 - r^2)\)
b) Sử dụng định lí Pythagore để tính chiều cao.
Áp dụng công thức tính thể tích hình nón \(V = \frac{1}{3}\pi {r^2}h.\)
Lời giải chi tiết
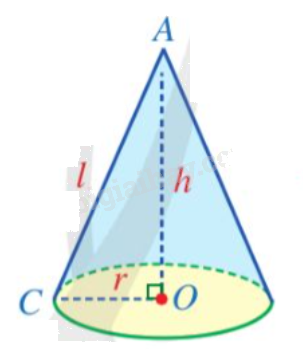
a) Gọi h là chiều cao, r là bán kính đáy, l là đường sinh chiếc mũ.
Bán kính đáy chiếc mũ là:
\(r = \left( {26 - 3.2} \right):2 = 10\left( {cm} \right).\)
Mặt ngoài là diện tích xung quanh chiếc mũ, ta có:
\({S_{xq}} = \pi rl = \pi .10.30 \approx 942\left( {c{m^2}} \right).\)
Bán kính của đường viền lớn bên ngoài vành mũ là:
\(26:2 = 13 (cm)\)
Diện tích phần vành mũ là:
\(\pi(13^2 - 10^2) \approx 216,66 (cm)\)
Vậy để phủ kín mặt ngoài chiếc mũ của chú hề như Hình 27b cần khoảng:
\(942 + 216,66 = 1158,66 \approx 1159\) \(c{m^2}\) giấy màu.
b) Chiều cao của chiếc mũ hình nón là:
\(\sqrt {30^2 - 10^2} = 20 \sqrt 2 (cm)\)
Thể tích phần có dạng hình nón của chiếc mũ chú hề là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.10^2}.20 \sqrt 2 \approx 2960,42 (c{m^3}).\)
Vậy thể tích phần có dạng hình nón của chiếc mũ chú hề ở Hình 27b khoảng \(2960,42 (c{m^3}).\)
Bài tập 4 trang 103 SGK Toán 9 tập 2 - Cánh diều là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về hàm số bậc hai và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này, cùng với những lưu ý quan trọng để đạt kết quả tốt nhất.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài tập 4, chúng ta cần xác định hàm số bậc hai, tìm tọa độ đỉnh, trục đối xứng và vẽ đồ thị của hàm số đó.
Đề bài: Cho hàm số y = x2 - 4x + 3. Hãy xác định tọa độ đỉnh, trục đối xứng và vẽ đồ thị của hàm số.
Giải:
Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 4 trang 103 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai và ứng dụng của nó. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.