Chào mừng các em học sinh đến với lời giải chi tiết bài tập 4 trang 123 SGK Toán 9 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 4 thuộc chương trình học Toán 9 tập 1, tập trung vào việc rèn luyện kỹ năng giải toán về một số chủ đề quan trọng.
Khi đóng đáy thuyền cho những con thuyền vượt biển, người Vikigns sử dụng hai loại nêm: nêm góc và nêm cong (lần lượt tô màu xanh, màu đỏ trong Hình 89). Mặt cắt (ABCD) của nêm góc có dạng hai tam giác vuông (OAE,ODE) bằng nhau với cạnh huyền chung và bỏ đi hình quạt tròn (OBC)(Hình 90), được làm từ những thân cây mọc thẳng. Mặt cắt (MNPQ) của nêm cong có dạng một phần của hình vành khuyên (Hình 91), được làm từ những thân cây cong. Kích thước của nêm cong được cho như ở Hình 91. a) Diệ
Đề bài
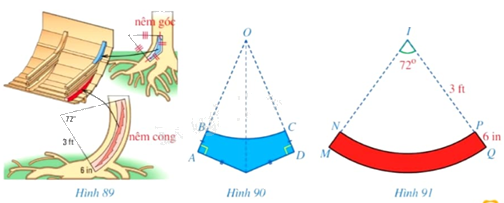
Khi đóng đáy thuyền cho những con thuyền vượt biển, người Vikigns sử dụng hai loại nêm: nêm góc và nêm cong (lần lượt tô màu xanh, màu đỏ trong Hình 89). Mặt cắt \(ABCD\) của nêm góc có dạng hai tam giác vuông \(OAE,ODE\) bằng nhau với cạnh huyền chung và bỏ đi hình quạt tròn \(OBC\)(Hình 90), được làm từ những thân cây mọc thẳng. Mặt cắt \(MNPQ\) của nêm cong có dạng một phần của hình vành khuyên (Hình 91), được làm từ những thân cây cong. Kích thước của nêm cong được cho như ở Hình 91.
a) Diện tích của nêm cong là bao nhiêu centimét vuông (lấy 1 ft = 30,48cm, 1 in = 2,54cm, \(\pi = 3,14\) và làm tròn kết quả đến hàng đơn vị)?
b) Cần phải biết những kích thước nào của nêm góc để tính được diện tích của nêm đó?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Dựa vào kiến thức đã học để tính.
b) Dựa vào công thức: diện tích nêm góc = diện tích 2 tam giác - diện tích hình quạt OBC.
Lời giải chi tiết
a) Đổi \(3ft = 3.30,48 = 91,44cm\)
\(6in = 6.2,54 = 15,24 cm\)
+ Diện tích quạt tròn \(INP\) là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.91,44}^2}.72}}{{360}} \approx 5254\left( {c{m^2}} \right)\)
+ Diện tích quạt tròn \(IMQ\) là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{\left( {91,44 + 15,24)} \right)}^2}.72}}{{360}} \approx 7151\left( {c{m^2}} \right)\)
+ Diện tích của nêm cong là:
\(S = {S_{IMQ}} - {S_{INP}} \approx 7151 - 5254 \approx 1897\left( {c{m^2}} \right)\)
b) Diện tích nêm góc = diện tích 2 tam giác - diện tích hình quạt OBC.
\(S_{2\Delta} = 2.\frac{1}{2} OA.OE = OA.OE\)
\(S_{OBC} = \frac{\pi.OB^2.\widehat{BOC}}{360}\)
\(S_{nêm\;góc} = OA.AE - \frac{\pi.OB^2.\widehat{BOC}}{360}\)
Vậy để tính được diện tích của nêm góc cần biết: góc \(BOC\), cạnh OB, OA (hoặc AE).
Bài tập 4 trang 123 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế. Để giúp các em hiểu rõ hơn về bài tập này, giaitoan.edu.vn xin giới thiệu hướng dẫn chi tiết và phương pháp giải như sau:
Trước khi bắt đầu giải bài tập, chúng ta cần phân tích đề bài một cách cẩn thận để xác định rõ yêu cầu và các dữ kiện đã cho. Bài tập 4 trang 123 SGK Toán 9 tập 1 - Cánh diều thường yêu cầu học sinh:
Tùy thuộc vào từng dạng bài tập cụ thể, chúng ta có thể áp dụng các phương pháp giải khác nhau. Một số phương pháp thường được sử dụng trong việc giải bài tập Toán 9 tập 1 - Cánh diều bao gồm:
(Nội dung lời giải chi tiết cho từng ý của bài tập 4 sẽ được trình bày tại đây. Ví dụ:)
a) Ý a:
Để giải ý a, ta thực hiện các bước sau:
Kết quả: ...
b) Ý b:
Tương tự như ý a, ta thực hiện các bước sau:
Kết quả: ...
Để giúp các em hiểu rõ hơn về phương pháp giải, chúng ta cùng xem xét một ví dụ minh họa sau:
Ví dụ: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Lời giải:
Áp dụng định lý Pitago vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42 = 9 + 16 = 25
BC = √25 = 5cm
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 9 tập 1 - Cánh diều và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên giaitoan.edu.vn để luyện tập thêm.
Bài tập 4 trang 123 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng, giúp các em rèn luyện kỹ năng giải toán và củng cố kiến thức đã học. Hy vọng với hướng dẫn chi tiết và phương pháp giải mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.
| Bài tập | Lời giải |
|---|---|
| Bài tập 1 | Link đến lời giải bài tập 1 |
| Bài tập 2 | Link đến lời giải bài tập 2 |