Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 7 trang 42 sách giáo khoa Toán 9 tập 2 của nhà xuất bản Cánh diều.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng để giúp bạn nắm vững kiến thức.
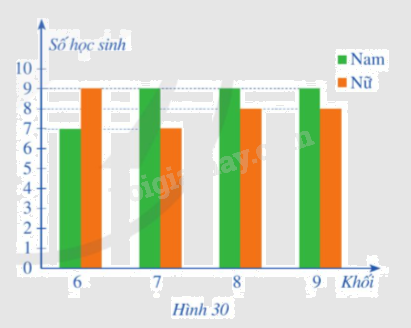
Biểu đồ cột kép ở Hình 30 biểu diễn số lượng học sinh tham gia thi giải thi đấu thể thao của một trường THCS. Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó. Tính xác suất của mỗi biến cố sau: A: “Học sinh được chọn là nam”. B: “Học sinh được chọn thuộc khối 6”. C: “Học sinh được chọn là nữ và không thuộc khối 9”.
Đề bài
Biểu đồ cột kép ở Hình 30 biểu diễn số lượng học sinh tham gia thi giải thi đấu thể thao của một trường THCS.
Chọn ngẫu nhiên một học sinh tham gia giải thi đấu thể thao của trường đó.
Tính xác suất của mỗi biến cố sau:
A: “Học sinh được chọn là nam”.
B: “Học sinh được chọn thuộc khối 6”.
C: “Học sinh được chọn là nữ và không thuộc khối 9”.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Bước 1: Lập bảng thống kê
Bước 2: Tính xác suất của mỗi biến cố

Lời giải chi tiết
Bảng thống kê:
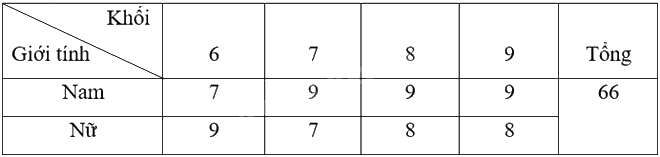
- Có 7 + 9 + 9 + 9 = 34 học sinh nam.
Xác suất của biến cố A: “Học sinh được chọn là nam” là:
\(P(A) = \frac{{34}}{{66}} = \frac{{17}}{{33}}\)
- Có 7 + 9 = 16 học sinh khối 6.
Xác suất của biến cố B: “Học sinh được chọn là học sinh khối 6” là:
\(P(B) = \frac{{16}}{{66}} = \frac{8}{{33}}\)
- Có 9 + 7 + 8 = 24 học sinh nữ không thuộc khối 9.
Xác suất của biến cố C: “Học sinh được chọn là nữ và không thuộc khối 9” là:
\(P(C) = \frac{{24}}{{66}} = \frac{4}{{11}}\)
Bài tập 7 trang 42 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hệ số góc và đường thẳng song song.
Bài tập 7 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để xác định hệ số góc của đường thẳng, ta cần đưa phương trình đường thẳng về dạng y = ax + b, trong đó a là hệ số góc.
Ví dụ: Cho đường thẳng 2x + 3y = 6. Ta có thể viết lại phương trình này như sau:
3y = -2x + 6
y = (-2/3)x + 2
Vậy hệ số góc của đường thẳng là -2/3.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song khi và chỉ khi a1 = a2 và b1 ≠ b2.
Ví dụ: Cho hai đường thẳng y = 2x + 1 và y = 2x - 3. Vì hệ số góc của hai đường thẳng bằng nhau (a1 = a2 = 2) và tung độ gốc khác nhau (b1 = 1 ≠ b2 = -3), nên hai đường thẳng này song song.
Để viết phương trình đường thẳng thỏa mãn các điều kiện cho trước, ta cần xác định hệ số góc và tung độ gốc của đường thẳng.
Ví dụ: Viết phương trình đường thẳng đi qua điểm A(1; 2) và song song với đường thẳng y = 3x + 1.
Vì đường thẳng cần viết song song với đường thẳng y = 3x + 1, nên hệ số góc của nó cũng là 3. Vậy phương trình đường thẳng có dạng y = 3x + b.
Thay tọa độ điểm A(1; 2) vào phương trình, ta được:
2 = 3(1) + b
b = -1
Vậy phương trình đường thẳng cần viết là y = 3x - 1.
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 9 tập 2 - Cánh diều hoặc các bài tập trực tuyến trên giaitoan.edu.vn.
Bài tập 7 trang 42 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!