Chào mừng các em học sinh đến với lời giải chi tiết bài tập 4 trang 110 SGK Toán 9 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 4 thuộc chương trình học Toán 9 tập 1, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Chúng tôi hy vọng với những hướng dẫn chi tiết này, các em sẽ hiểu rõ hơn về cách tiếp cận và giải quyết các bài toán tương tự.
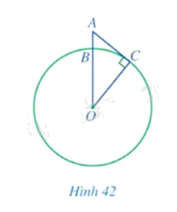
Một người quan sát đặt mắt ở vị trí (A) có độ cao cách mực nước biển là (AB = 5m). Cắt bề mặt Trái Đất bởi một mặt phẳng đi qua điểm (A) và tâm của Trái Đất thì phần chung giữa chúng là một đường tròn lớn tâm (O) như Hình 42. Tầm quan sát tối đa từ vị trí (A) là đoạn (AC), trong đó (C) là tiếp điểm của tiếp tuyến đi qua (A) với đường tròn (left( O right)). Tính độ dài đoạn thẳng (AC) (theo đơn vị kilômét và làm tròn kết quả đến hàng phần mười), biết bán kính Trái Đất là: (
Đề bài
Một người quan sát đặt mắt ở vị trí \(A\) có độ cao cách mực nước biển là \(AB = 5m\). Cắt bề mặt Trái Đất bởi một mặt phẳng đi qua điểm \(A\) và tâm của Trái Đất thì phần chung giữa chúng là một đường tròn lớn tâm \(O\) như Hình 42. Tầm quan sát tối đa từ vị trí \(A\) là đoạn \(AC\), trong đó \(C\) là tiếp điểm của tiếp tuyến đi qua \(A\) với đường tròn \(\left( O \right)\). Tính độ dài đoạn thẳng \(AC\) (theo đơn vị kilômét và làm tròn kết quả đến hàng phần mười), biết bán kính Trái Đất là: \(OB = OC \approx 6400km\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào tính chất tiếp tuyến để chứng minh.
Lời giải chi tiết
Ta có: \(AO = AB + BO \approx \frac{5}{{1000}} + 6400 \approx 6400,005\left( {km} \right)\).
Áp dụng định lý Pythagore vào tam giác \(AOC\) vuông tại \(C\) có:
\(\begin{array}{l}A{C^2} + O{C^2} = A{O^2} \Rightarrow A{C^2} = A{O^2} - O{C^2} \approx 6400,{005^2} - {6400^2} \approx 64,000025\\ \Rightarrow AC \approx 8\left( {km} \right).\end{array}\)
Bài tập 4 trang 110 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và ứng dụng của nó vào giải quyết các bài toán thực tế. Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, giaitoan.edu.vn xin trình bày hướng dẫn chi tiết và phương pháp giải như sau:
(Nội dung đề bài sẽ được trình bày đầy đủ tại đây)
Trước khi bắt đầu giải bài tập, chúng ta cần phân tích đề bài để hiểu rõ yêu cầu và xác định các yếu tố quan trọng. Trong bài tập 4 này, chúng ta cần:
Để giải bài tập 4 trang 110 SGK Toán 9 tập 1 - Cánh diều, chúng ta có thể áp dụng các phương pháp sau:
(Lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, giải thích rõ ràng và kết quả cuối cùng)
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập 4 trang 110 SGK Toán 9 tập 1 - Cánh diều, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự:
Ví dụ 1:(Nội dung ví dụ 1)
Bài tập 1:(Nội dung bài tập 1)
Khi giải bài tập 4 trang 110 SGK Toán 9 tập 1 - Cánh diều, các em cần lưu ý những điều sau:
Bài tập 4 trang 110 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng, giúp các em học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng của nó. Hy vọng với hướng dẫn chi tiết và phương pháp giải mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.
Chúc các em học tốt!