Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 95 SGK Toán 9 tập 2 - Cánh diều tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục 3 trang 95 tập trung vào các kiến thức về hàm số bậc nhất và ứng dụng của nó.
a) Nêu công thức tính thể tích hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ (Hình 7) khi biết diện tích đáy và chiều cao. b) Cũng như hình lăng trụ đứng tứ giác, mỗi hình trụ đều có thể tích. Hãy dự đoán cách tính thể tích của hình trụ (Hình 8).
Đề bài
Trả lời câu hỏi Hoạt động 4 trang 95SGK Toán 9 Cánh diều
a) Nêu công thức tính thể tích hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ (Hình 7) khi biết diện tích đáy và chiều cao.
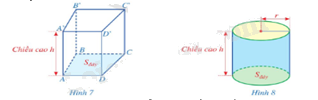
b) Cũng như hình lăng trụ đứng tứ giác, mỗi hình trụ đều có thể tích. Hãy dự đoán cách tính thể tích của hình trụ (Hình 8).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Nhớ lại công thức lớp 8.
b) Dựa vào các thông số đề bài đã cho: Sđáy và chiều cao.
Lời giải chi tiết
a) Diện tích hình lăng trụ đứng tứ giác: Sđáy.h
b) Dự đoán: Shình trụ = Sđáy.h = \(\pi {r^2}h.\)
Mục 3 trang 95 SGK Toán 9 tập 2 - Cánh diều là một phần quan trọng trong chương trình học Toán 9, tập trung vào việc củng cố kiến thức về hàm số bậc nhất. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, từ đó nâng cao khả năng tư duy logic và kỹ năng giải quyết vấn đề.
Mục 3 trang 95 bao gồm các bài tập liên quan đến:
Để giải tốt các bài tập trong Mục 3 trang 95, học sinh cần nắm vững các kiến thức sau:
Lời giải:
Vì đồ thị hàm số y = ax đi qua điểm A(2; 4) nên ta có:
4 = a * 2
=> a = 2
Vậy, hệ số a của hàm số là 2.
Lời giải:
Để vẽ đồ thị hàm số y = 2x - 1, ta cần xác định hai điểm thuộc đồ thị. Ví dụ:
Vẽ đường thẳng đi qua hai điểm A(0; -1) và B(1; 1), ta được đồ thị hàm số y = 2x - 1.
Một người đi xe đạp với vận tốc 15km/h. Hãy viết hàm số biểu thị quãng đường đi được của người đó theo thời gian đi.
Lời giải:
Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km). Ta có hàm số:
y = 15x
Hàm số này biểu thị mối quan hệ tuyến tính giữa quãng đường đi được và thời gian đi của người đó.
Hy vọng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập trong Mục 3 trang 95 SGK Toán 9 tập 2 - Cánh diều. Chúc các em học tập tốt!