Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3 trang 103 SGK Toán 9 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 3 thuộc chương trình học Toán 9 tập 2, tập trung vào việc vận dụng các kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Chúng tôi sẽ hướng dẫn các em từng bước để hiểu rõ bản chất của bài toán và cách tiếp cận phù hợp.
Phần mái lá của một ngôi nhà có dạng hình nón (không có đáy) với đường kính đáy khoảng 12 m và độ dài đường sinh khoảng 8,5 m (Hình 26). Chi phí để làm phần mái lá đó là 250 000 đồng/1 m2. Hỏi tổng chi phí để làm toàn bộ phần mái nhà đó là bao nhiêu đồng?
Đề bài
Phần mái lá của một ngôi nhà có dạng hình nón (không có đáy) với đường kính đáy khoảng 12 m và độ dài đường sinh khoảng 8,5 m (Hình 26). Chi phí để làm phần mái lá đó là 250 000 đồng/1 \(m^2\). Hỏi tổng chi phí để làm toàn bộ phần mái nhà đó là bao nhiêu đồng?

Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Bước 1: Tính diện tích xung quanh.
Bước 2: Tổng chi phí = diện tích xung quanh x 250.000 (đồng)
Lời giải chi tiết
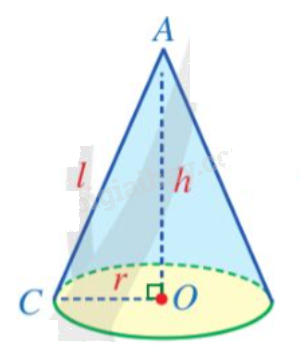
Phần mái lá của một ngôi nhà được biểu diễn dạng hình học như hình sau:
Bán kính đáy là: \(12:2 = 6\left( m \right).\)
Diện tích xung quanh của mái lá là:
\({S_{xq}} = \pi rl = \pi .6.8,5 \approx 160,14\left( {{m^2}} \right).\)
Tổng chi phí để làm toàn bộ phần mái nhà đó là:
\(160,14.250000 = 40.035.000\)(đồng).
Vậy tổng chi phí để làm toàn bộ phần mái nhà đó là \(40.035.000\) đồng.
Bài tập 3 trang 103 SGK Toán 9 tập 2 - Cánh diều yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết một bài toán thực tế liên quan đến quỹ đạo của một vật được ném lên. Để giải bài tập này, chúng ta cần xác định được phương trình hàm số bậc hai mô tả quỹ đạo của vật và sau đó tìm các điểm quan trọng trên quỹ đạo đó.
Đề bài thường mô tả một tình huống cụ thể, ví dụ như một quả bóng được ném lên từ một vị trí nhất định với một vận tốc ban đầu. Yêu cầu của bài toán thường là tìm độ cao cực đại của quả bóng, khoảng cách mà quả bóng bay được, hoặc thời gian để quả bóng chạm đất.
Để xây dựng phương trình hàm số bậc hai, chúng ta cần xác định các hệ số a, b, và c. Trong bài toán này, hệ số a thường liên quan đến gia tốc trọng trường (g = -9.8 m/s²), hệ số b liên quan đến vận tốc ban đầu (v₀), và hệ số c liên quan đến độ cao ban đầu (h₀). Phương trình tổng quát có dạng:
y = ax² + bx + c
Tọa độ đỉnh của parabol là điểm quan trọng nhất trên quỹ đạo của vật, vì nó cho biết độ cao cực đại mà vật đạt được. Tọa độ đỉnh (x₀, y₀) được tính bằng công thức:
Sau khi đã có phương trình hàm số bậc hai và tọa độ đỉnh, chúng ta có thể giải quyết các bài toán cụ thể được đặt ra trong đề bài. Ví dụ, để tìm thời gian để quả bóng chạm đất, chúng ta cần giải phương trình y = 0.
Giả sử một quả bóng được ném lên từ độ cao 1.5m với vận tốc ban đầu 10m/s. Phương trình quỹ đạo của quả bóng là:
y = -4.9x² + 10x + 1.5
Trong đó:
Tọa độ đỉnh của parabol là:
Vậy độ cao cực đại của quả bóng là khoảng 6.63m.
Khi giải các bài toán liên quan đến hàm số bậc hai, cần chú ý đến đơn vị đo lường và đảm bảo rằng tất cả các giá trị đều được biểu diễn trong cùng một đơn vị. Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính hợp lý của nó.
Bài tập 3 trang 103 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về ứng dụng của hàm số bậc hai trong thực tế. Bằng cách nắm vững các kiến thức và kỹ năng đã được trình bày trong bài viết này, các em có thể tự tin giải quyết các bài toán tương tự một cách hiệu quả.