Chào mừng các em học sinh đến với lời giải chi tiết bài tập 6 trang 74 SGK Toán 9 tập 2 - Cánh diều. Bài tập này thuộc chương trình học Toán 9, tập trung vào việc rèn luyện kỹ năng giải bài toán thực tế và áp dụng kiến thức đã học.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho tứ giác ABCD có các tam giác ABC và ACD lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N (Hình 17). Chứng minh: a) Ba điểm I, H, K thẳng hàng. b) AM = AN. c) (widehat {IAK} = frac{1}{2}widehat {BAD}.)
Đề bài
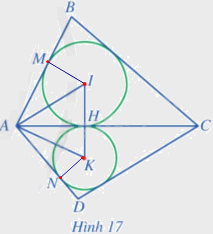
Cho tứ giác ABCD có các tam giác ABC và ACD lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N (Hình 17). Chứng minh:
a) Ba điểm I, H, K thẳng hàng.
b) AM = AN.
c) \(\widehat {IAK} = \frac{1}{2}\widehat {BAD}.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\widehat {IHA} + \widehat {AHK} = \widehat {IHK} = 90^\circ + 90^\circ = 180^\circ \).
b) Sử dụng tính chất hai tiếp tuyến cắt nhau suy ra AM = AN ( = AH).
c) Sử dụng tính chất hai tiếp tuyến cắt nhau suy ra điều phải chứng minh.
Lời giải chi tiết
a) Do đường tròn (I) nội tiếp tam giác ABC và tiếp xúc với đường thẳng AC tại H nên \(IH \bot AC\), suy ra \(\widehat {IHA} = 90^\circ .\)
Do đường tròn (K) nội tiếp tam giác ADC và tiếp xúc với đường thẳng AC tại H nên \(KH \bot AC\), suy ra \(\widehat {IHK} = 90^\circ .\)
Ta có: \(\widehat {IHA} + \widehat {AHK} = \widehat {IHK} = 90^\circ + 90^\circ = 180^\circ \), nên I, H, K thẳng hàng.
b) Xét đường tròn (I) có hai tiếp tuyến AB, AC cắt nhau tại A nên AM = AH (tính chất hai tiếp tuyến cắt nhau)
Xét đường tròn (K) có hai tiếp tuyến AC, AD cắt nhau tại A nên AN = AH (tính chất hai tiếp tuyến cắt nhau)
Suy ra AM = AN ( = AH).
c) Xét đường tròn (I) có hai tiếp tuyến AB, AC nên AI là phân giác của góc BAC suy ra \(\widehat {IAH} = \frac{1}{2} \widehat {BAC}\)
Xét đường tròn (K) có hai tiếp tuyến AC, AD nên AK là phân giác của góc DAC suy ra \(\widehat {KAH} = \frac{1}{2} \widehat {DAC}\)
Ta có:
\(\widehat {IAK} = \widehat {IAH} + \widehat {KAH} \)
\(= \frac{1}{2} \widehat {BAC} + \frac{1}{2} \widehat {DAC}\)
\(= \frac{1}{2} (\widehat {BAC} + \widehat {DAC})\)
\(= \frac{1}{2}\widehat {BAD}.\)
Hay \(\widehat {IAK} = \frac{1}{2}\widehat {BAD}.\)
Bài tập 6 trang 74 SGK Toán 9 tập 2 - Cánh diều là một bài toán thực tế, yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc hai để giải quyết. Để hiểu rõ hơn về bài toán này, chúng ta sẽ cùng nhau phân tích đề bài, tìm hiểu phương pháp giải và xem xét lời giải chi tiết.
Đề bài yêu cầu chúng ta giải một bài toán liên quan đến việc tìm chiều dài và chiều rộng của một mảnh đất hình chữ nhật, dựa vào thông tin về chu vi và diện tích của mảnh đất đó. Bài toán này đòi hỏi học sinh phải nắm vững kiến thức về hệ phương trình bậc hai và cách giải hệ phương trình đó.
Để giải bài tập này, chúng ta sẽ sử dụng phương pháp giải hệ phương trình bậc hai bằng phương pháp thế hoặc phương pháp cộng đại số. Cụ thể, chúng ta sẽ đặt ẩn cho chiều dài và chiều rộng của mảnh đất, sau đó lập hệ phương trình dựa trên thông tin về chu vi và diện tích của mảnh đất. Tiếp theo, chúng ta sẽ giải hệ phương trình đó để tìm ra giá trị của các ẩn, từ đó tìm được chiều dài và chiều rộng của mảnh đất.
Đề bài: Một mảnh đất hình chữ nhật có chu vi là 50m và diện tích là 150m2. Tính chiều dài và chiều rộng của mảnh đất.
Giải:
Khi giải bài tập về hệ phương trình bậc hai, các em cần lưu ý những điều sau:
Để rèn luyện kỹ năng giải bài tập về hệ phương trình bậc hai, các em có thể tham khảo một số bài tập tương tự sau:
Bài tập 6 trang 74 SGK Toán 9 tập 2 - Cánh diều là một bài toán quan trọng, giúp các em củng cố kiến thức về hệ phương trình bậc hai và rèn luyện kỹ năng giải bài toán thực tế. Hy vọng rằng, với hướng dẫn chi tiết và phương pháp giải trên, các em sẽ tự tin giải quyết bài toán này và đạt kết quả tốt trong môn Toán.