Chào mừng các em học sinh đến với lời giải chi tiết Bài 1 trang 35 SGK Toán 8 tập 2 – Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, cập nhật và phù hợp với chương trình học Toán 8 hiện hành.
Trong Hình 4,
Đề bài
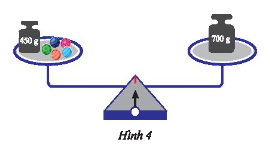
Trong Hình 4, cho biết các viên bi có cùng khối lượng là \(x\left( g \right)\) và cân bằng. Viết phương trình biểu diễn liên hệ giữa khối lượng của các vật ở hai đĩa cân.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Do khối lượng hai đĩa cân bằng nhau nên ta có biểu thức biểu thị mối quan hệ giữa hai đĩa cân. Khi đó, ta có phương trình biểu diễn mối liên hệ giữa khối lượng các vật ở hai đĩa cân
Lời giải chi tiết
Trên đĩa cân bên trái ta thấy có 1 quả có khối lượng \(450\) gam và 5 viên bi có khối lượng \(x\) gam nên khối lượng đĩa cân bên trái là: \(450 + x + x + x + x + x\) (gam)
Trên đĩa cân bên phải ta thấy có 1 quả cân khối lượng \(700\) gam nên khối lượng đĩa cân bên phải là: 700 gam.
Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:
\(450 + x + x + x + x + x = 700\) hay \(5x + 450 = 700\).
Vậy phương trình biểu diễn sự thăng bằng là \(5x + 450 = 700\).
Bài 1 trang 35 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững các kiến thức lý thuyết cơ bản về hình thang cân, bao gồm:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây, ví dụ: Cho hình thang cân ABCD có AB // CD, AD = BC. Gọi E là giao điểm của AC và BD. Chứng minh rằng: a) ΔADC = ΔBCD; b) EA = EB.)
Để chứng minh hai tam giác bằng nhau, chúng ta cần chỉ ra sự bằng nhau của các cạnh và góc tương ứng. Trong trường hợp này:
Vậy, theo trường hợp cạnh - cạnh - góc (c-c-g), ta có ΔADC = ΔBCD.
Sau khi chứng minh được ΔADC = ΔBCD, ta suy ra AC = BD (các cạnh tương ứng). Xét hai tam giác ADE và BCE, ta có:
Vậy, theo trường hợp góc - cạnh - góc (g-c-g), ta có ΔADE = ΔBCE. Suy ra EA = EB (các cạnh tương ứng).
Để củng cố kiến thức về hình thang cân và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo các bài tập tương tự sau:
Để học tốt môn Toán 8, các em cần:
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!