Chào mừng các em học sinh đến với lời giải chi tiết Bài 1 trang 9 SGK Toán 8 – Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, với đội ngũ giáo viên giàu kinh nghiệm và nội dung được cập nhật liên tục.
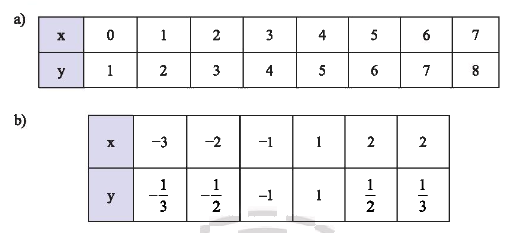
Các giá trị tương ứng của hai đại lượng (x) và (y) được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng (y) có phải là hàm số của đại lượng (x) không? Giải thích.
Đề bài
Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không? Giải thích.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Quan sát các bảng sau đó sử dụng định nghĩa về hàm số để giải thích và đưa ra kết luận
Nếu đại lượng \(y\) phụ thuộc vào một đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x\) ta luôn xác định được duy nhất một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của biến số \(x\).
Lời giải chi tiết
a) Bảng a đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).
Bài 1 trang 9 SGK Toán 8 – Chân trời sáng tạo thuộc chương 1: Số hữu tỉ. Bài tập này yêu cầu học sinh vận dụng kiến thức về số hữu tỉ, biểu diễn số hữu tỉ trên trục số, và so sánh các số hữu tỉ để giải quyết các bài toán cụ thể.
Bài 1 gồm các câu hỏi nhỏ, yêu cầu học sinh thực hiện các thao tác sau:
Để liệt kê các số hữu tỉ theo thứ tự tăng dần, ta cần chuyển đổi chúng về cùng một dạng (ví dụ: phân số hoặc số thập phân). Sau đó, so sánh các giá trị và sắp xếp theo thứ tự từ nhỏ đến lớn.
Sắp xếp các số hữu tỉ theo thứ tự tăng dần: -2,5; -2; -1,2; 0; 0,75; 1,5
Để biểu diễn một số hữu tỉ trên trục số, ta cần xác định vị trí của nó so với các điểm đã biết (ví dụ: 0, 1, -1). Sau đó, đánh dấu điểm tương ứng trên trục số.
Ví dụ: Để biểu diễn -3/2 trên trục số, ta thấy rằng -3/2 = -1,5. Do đó, ta tìm điểm -1,5 trên trục số và đánh dấu nó.
Để so sánh hai số hữu tỉ, ta có thể sử dụng một trong các phương pháp sau:
Ví dụ: Để so sánh -2/3 và 1/4, ta chuyển đổi chúng về số thập phân:
Vì -0,67 < 0,25 nên -2/3 < 1/4.
Để củng cố kiến thức về số hữu tỉ, các em có thể làm thêm các bài tập tương tự trong SGK Toán 8 – Chân trời sáng tạo hoặc các tài liệu tham khảo khác.
Bài 1 trang 9 SGK Toán 8 – Chân trời sáng tạo là một bài tập cơ bản, giúp học sinh làm quen với các khái niệm về số hữu tỉ và rèn luyện kỹ năng giải bài tập. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em sẽ tự tin hơn khi học môn Toán.