Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 31, 32 SGK Toán 8 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập này thuộc chương trình Toán 8 tập 2, tập trung vào việc rèn luyện kỹ năng giải toán và áp dụng kiến thức đã học vào thực tế.
a) Ở câu hỏi khởi động trên, viết các biểu thức biểu thị tổng khối lượng của các vật trên mỗi đĩa cân. Từ điểu kiện cân thăng bằng, hai biểu thức có mối quan hệ như thế nào? b) Nếu (x = 200)thì cân có cân bằng không? Tại sao? Nếu (x = 100) thì cân có cân bằng không? Tại sao?
Video hướng dẫn giải
Cho phương trình \(4t - 3 = 12 - t\). Trong hai số 3 và 5, có số nào là nghiệm của phương trình đã cho không?
Phương pháp giải:
Giá trị \({x_0}\)của biến \(x\) làm cho hai vế của phương trình bằng nhau được gọi là nghiệm của phương trình.
Lời giải chi tiết:
+ Với \(t = 3\) thay vào phương trình ta được
\(4.3 - 3 = 12 - 3\) hay \(9 = 9\) (đúng)
Do đó, \(t = 3\) là nghiệm của phương trình.
+ Với \(t = 5\) thay vào phương trình ta được
\(4.5 - 3 = 12 - 5\) hay \(17 = 7\) (sai)
Do đó, \(t = 5\) không là nghiệm của phương trình.
Video hướng dẫn giải
a) Ở câu hỏi khởi động trên, viết các biểu thức biểu thị tổng khối lượng của các vật trên mỗi đĩa cân. Từ điểu kiện cân thăng bằng, hai biểu thức có mối quan hệ như thế nào?
b) Nếu \(x = 200\)thì cân có cân bằng không? Tại sao?
Nếu \(x = 100\) thì cân có cân bằng không? Tại sao?
Phương pháp giải:
Tổng khối lượng của các vật trên mỗi đĩa cân bằng khối lượng các vật trên mỗi đĩa cân cộng lại.
Cân cân bằng thì khối lượng của đĩa cân bên trái bằng khối lượng đĩa cân bên phải.
Lời giải chi tiết:
a) Trên đĩa cân bên trái ta thấy có 4 quả cân, mỗi quả có khối lượng \(x\) gam nên khối lượng đĩa cân bên trái là: \(x + x + x + x\) (gam)
Trên đĩa cân bên phải ta thấy có 2 quả cân, một quả có khối lượng \(x\) gam và một quả có khối lượng 600 gam nên khối lượng đĩa cân bên phải là: \(x + 600\) gam.
Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:
\(x + x + x + x = x + 600\) hay \(4x = 600 + x\)
b) Nếu \(x = 200\) thì khối lượng đĩa cân bên trái là: \(4.200 = 800\) (gam); khối lượng đĩa cân bên phải là \(200 + 600 = 800\) (gam).
Do đó, cân thăng bằng.
Nếu \(x = 100\) thì khối lượng đĩa cân bên trái là: \(4.100 = 400\) (gam); khối lượng đĩa cân bên phải là \(100 + 600 = 700\) (gam).
Do đó, cân không thăng bằng.
Video hướng dẫn giải
Đặt lên hai đĩa cân những quả cân như Hình 1.
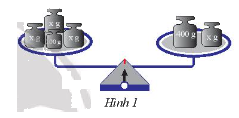
a) Biết rằng cân thăng bằng, hãy viết phương trình biểu thị sự thăng bằng này.
b) Nếu \(x = 100\) cân có thăng bằng không? Vì sao?
Nếu \(x = 150\) thì cân có thăng bằng không? Vì sao?
Từ đó, chỉ ra một nghiệm của phương trình ở câu a.
Phương pháp giải:
Tổng khối lượng của các vật trên mỗi đĩa cân bằng khối lượng các vật trên mỗi đĩa cân cộng lại.
Cân cân bằng thì khối lượng của đĩa cân bên trái bằng khối lượng đĩa cân bên phải.
Lời giải chi tiết:
a) Trên đĩa cân bên trái ta thấy có 4 quả cân, có 3 quả có khối lượng \(x\) gam và 1 quả có khối lượng 100 gam nên khối lượng đĩa cân bên trái là: \(x + x + x + 100\) (gam)
Trên đĩa cân bên phải ta thấy có 2 quả cân, 1 quả có khối lượng \(x\) gam và một quả có khối lượng 400 gam nên khối lượng đĩa cân bên phải là: \(x + 400\) gam.
Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:
\(x + x + x + 100 = x + 400\) hay \(3x + 100 = 400 + x\).
Vậy phương trình biểu diễn sự thăng bằng là \(3x + 100 = 400 + x\).
b) Nếu \(x = 100\) thì khối lượng đĩa cân bên trái là: \(3.100 + 100 = 300 + 100 = 400\) (gam); khối lượng đĩa cân bên phải là \(400 + 100 = 500\) (gam).
Do đó, cân không thăng bằng.
Nếu \(x = 150\) thì khối lượng đĩa cân bên trái là: \(3.150 + 100 = 550\) (gam); khối lượng đĩa cân bên phải là \(150 + 400 = 550\) (gam).
Do đó, cân thăng bằng.
Video hướng dẫn giải
a) Ở câu hỏi khởi động trên, viết các biểu thức biểu thị tổng khối lượng của các vật trên mỗi đĩa cân. Từ điểu kiện cân thăng bằng, hai biểu thức có mối quan hệ như thế nào?
b) Nếu \(x = 200\)thì cân có cân bằng không? Tại sao?
Nếu \(x = 100\) thì cân có cân bằng không? Tại sao?
Phương pháp giải:
Tổng khối lượng của các vật trên mỗi đĩa cân bằng khối lượng các vật trên mỗi đĩa cân cộng lại.
Cân cân bằng thì khối lượng của đĩa cân bên trái bằng khối lượng đĩa cân bên phải.
Lời giải chi tiết:
a) Trên đĩa cân bên trái ta thấy có 4 quả cân, mỗi quả có khối lượng \(x\) gam nên khối lượng đĩa cân bên trái là: \(x + x + x + x\) (gam)
Trên đĩa cân bên phải ta thấy có 2 quả cân, một quả có khối lượng \(x\) gam và một quả có khối lượng 600 gam nên khối lượng đĩa cân bên phải là: \(x + 600\) gam.
Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:
\(x + x + x + x = x + 600\) hay \(4x = 600 + x\)
b) Nếu \(x = 200\) thì khối lượng đĩa cân bên trái là: \(4.200 = 800\) (gam); khối lượng đĩa cân bên phải là \(200 + 600 = 800\) (gam).
Do đó, cân thăng bằng.
Nếu \(x = 100\) thì khối lượng đĩa cân bên trái là: \(4.100 = 400\) (gam); khối lượng đĩa cân bên phải là \(100 + 600 = 700\) (gam).
Do đó, cân không thăng bằng.
Video hướng dẫn giải
Cho phương trình \(4t - 3 = 12 - t\). Trong hai số 3 và 5, có số nào là nghiệm của phương trình đã cho không?
Phương pháp giải:
Giá trị \({x_0}\)của biến \(x\) làm cho hai vế của phương trình bằng nhau được gọi là nghiệm của phương trình.
Lời giải chi tiết:
+ Với \(t = 3\) thay vào phương trình ta được
\(4.3 - 3 = 12 - 3\) hay \(9 = 9\) (đúng)
Do đó, \(t = 3\) là nghiệm của phương trình.
+ Với \(t = 5\) thay vào phương trình ta được
\(4.5 - 3 = 12 - 5\) hay \(17 = 7\) (sai)
Do đó, \(t = 5\) không là nghiệm của phương trình.
Video hướng dẫn giải
Đặt lên hai đĩa cân những quả cân như Hình 1.
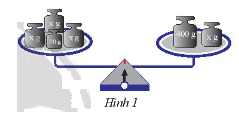
a) Biết rằng cân thăng bằng, hãy viết phương trình biểu thị sự thăng bằng này.
b) Nếu \(x = 100\) cân có thăng bằng không? Vì sao?
Nếu \(x = 150\) thì cân có thăng bằng không? Vì sao?
Từ đó, chỉ ra một nghiệm của phương trình ở câu a.
Phương pháp giải:
Tổng khối lượng của các vật trên mỗi đĩa cân bằng khối lượng các vật trên mỗi đĩa cân cộng lại.
Cân cân bằng thì khối lượng của đĩa cân bên trái bằng khối lượng đĩa cân bên phải.
Lời giải chi tiết:
a) Trên đĩa cân bên trái ta thấy có 4 quả cân, có 3 quả có khối lượng \(x\) gam và 1 quả có khối lượng 100 gam nên khối lượng đĩa cân bên trái là: \(x + x + x + 100\) (gam)
Trên đĩa cân bên phải ta thấy có 2 quả cân, 1 quả có khối lượng \(x\) gam và một quả có khối lượng 400 gam nên khối lượng đĩa cân bên phải là: \(x + 400\) gam.
Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:
\(x + x + x + 100 = x + 400\) hay \(3x + 100 = 400 + x\).
Vậy phương trình biểu diễn sự thăng bằng là \(3x + 100 = 400 + x\).
b) Nếu \(x = 100\) thì khối lượng đĩa cân bên trái là: \(3.100 + 100 = 300 + 100 = 400\) (gam); khối lượng đĩa cân bên phải là \(400 + 100 = 500\) (gam).
Do đó, cân không thăng bằng.
Nếu \(x = 150\) thì khối lượng đĩa cân bên trái là: \(3.150 + 100 = 550\) (gam); khối lượng đĩa cân bên phải là \(150 + 400 = 550\) (gam).
Do đó, cân thăng bằng.
Mục 1 trang 31, 32 SGK Toán 8 tập 2 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và các định nghĩa liên quan. Bài viết này sẽ cung cấp một cái nhìn tổng quan về nội dung chính của mục 1, đồng thời hướng dẫn chi tiết phương pháp giải các dạng bài tập thường gặp.
Thông thường, Mục 1 sẽ giới thiệu một khái niệm mới hoặc mở rộng kiến thức đã học. Ví dụ, nó có thể liên quan đến các phép biến đổi đại số, giải phương trình, bất phương trình, hoặc các bài toán hình học cơ bản. Việc hiểu rõ nội dung lý thuyết là bước đầu tiên quan trọng để giải quyết các bài tập một cách chính xác.
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1 trang 31, 32 SGK Toán 8 tập 2 Chân trời sáng tạo:
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải thích chi tiết từng bước giải, sử dụng công thức và lý thuyết liên quan)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải thích chi tiết từng bước giải, sử dụng công thức và lý thuyết liên quan)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải thích chi tiết từng bước giải, sử dụng công thức và lý thuyết liên quan)
Để giải các bài tập trong Mục 1 trang 31, 32 một cách nhanh chóng và hiệu quả, học sinh có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và kỹ năng giải toán, học sinh nên luyện tập thêm các bài tập tương tự. Các em có thể tìm thấy các bài tập luyện tập trong sách bài tập, trên các trang web học toán online hoặc trong các đề thi thử.
Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong Mục 1 trang 31, 32 SGK Toán 8 tập 2 Chân trời sáng tạo một cách hiệu quả. Chúc các em học tập tốt!