Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 9 trang 51 SGK Toán 8 tập 2 – Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập về nhà.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải cụ thể, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
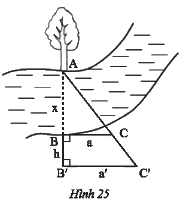
Quan sát Hình 25 và chứng minh
Đề bài
Quan sát Hình 25 và chứng minh: \(x = \frac{{ah}}{{a' - a}}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Hệ quả của định lí Thales.
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết
Vì \(\left\{ \begin{array}{l}BC \bot AB'\\B'C' \bot AB'\end{array} \right. \Rightarrow BC//B'C'\)(quan hệ từ vuông góc đến song song).
- Xét tam giác \(AB'C'\) có \(BC//B'C'\) và \(BC\) cắt \(AB';AC'\) lần lượt tại \(B;C\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AB'}} = \frac{{BC}}{{B'C'}} \Rightarrow \frac{x}{{x + h}} = \frac{a}{{a'}} \Rightarrow xa' = a\left( {x + h} \right) \Leftrightarrow xa' = ax + ah\)
\( \Leftrightarrow xa' - ax = ah \Leftrightarrow x\left( {a' - a} \right) = ah \Leftrightarrow x = \frac{{ah}}{{a' - a}}\) (điều phải chứng minh).
Bài 9 trang 51 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình hộp chữ nhật và hình lập phương để giải quyết các bài toán thực tế. Bài toán này yêu cầu học sinh phải hiểu rõ công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của các hình này.
Bài 9 yêu cầu học sinh giải các bài toán liên quan đến tính toán diện tích và thể tích của hình hộp chữ nhật và hình lập phương. Cụ thể, bài toán có thể yêu cầu tính:
Để giải bài 9 trang 51 SGK Toán 8 tập 2 – Chân trời sáng tạo, học sinh cần nắm vững các công thức sau:
Ngoài ra, học sinh cần chú ý đến việc đổi đơn vị đo khi cần thiết để đảm bảo tính chính xác của kết quả.
Ví dụ 1: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Tính diện tích xung quanh và thể tích của hình hộp chữ nhật đó.
Giải:
Ví dụ 2: Một hình lập phương có cạnh 2cm. Tính diện tích toàn phần và thể tích của hình lập phương đó.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về hình hộp chữ nhật và hình lập phương, học sinh có thể tự giải thêm các bài tập sau:
Khi giải bài tập về hình hộp chữ nhật và hình lập phương, học sinh nên:
Giaitoan.edu.vn hy vọng rằng với hướng dẫn chi tiết này, học sinh sẽ tự tin giải bài 9 trang 51 SGK Toán 8 tập 2 – Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| Diện tích xung quanh hình hộp chữ nhật | 2(a + b)h |
| Diện tích toàn phần hình hộp chữ nhật | 2(ab + ah + bh) |
| Thể tích hình hộp chữ nhật | abh |
| Diện tích toàn phần hình lập phương | 6a2 |
| Thể tích hình lập phương | a3 |