Chào mừng bạn đến với bài học lý thuyết về Hình chóp tam giác đều và Hình chóp tứ giác đều trong chương trình Toán 8 - Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hai loại hình chóp này.
Chúng ta sẽ cùng nhau tìm hiểu về định nghĩa, các yếu tố của hình chóp, cách tính diện tích xung quanh, diện tích toàn phần và thể tích của chúng. Bài học được trình bày một cách dễ hiểu, kèm theo nhiều ví dụ minh họa giúp bạn nắm bắt kiến thức một cách nhanh chóng và hiệu quả.
Hình chóp tam giác đều là gì?
1. Hình chóp tam giác đều
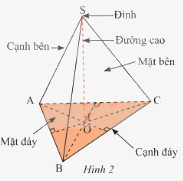
Hình chóp tam giác đều có:
- Đáy là tam giác đều.
- 3 cạnh bên bằng nhau.
- 3 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 3 cạnh đáy bằng nhau là ba cạnh của tam giác đáy.
- Chân đường cao trùng với tâm của đáy.
2. Hình chóp tứ giác đều
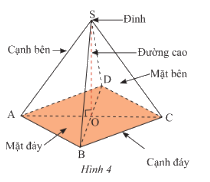
Hình chóp tứ giác đều có:
- Đáy là hình vuông.
- 4 cạnh bên bằng nhau.
- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.
- Chân đường cao trùng với giao điểm của hai đường chéo của mặt đáy.
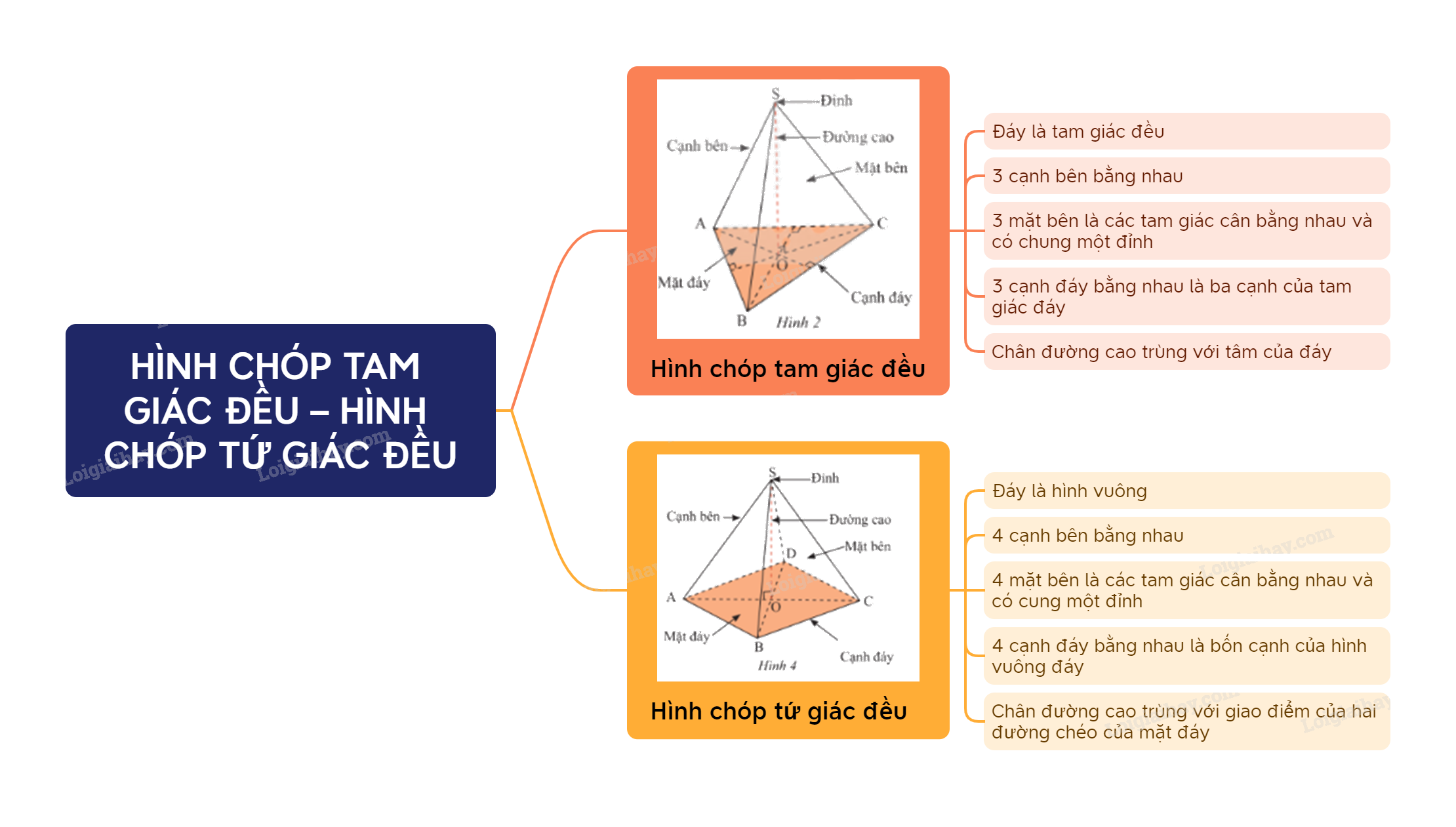
Hình chóp là một trong những hình khối quan trọng trong chương trình Hình học không gian lớp 8. Việc nắm vững lý thuyết về hình chóp, đặc biệt là hình chóp tam giác đều và hình chóp tứ giác đều, là nền tảng để giải quyết các bài toán thực tế và tiếp thu kiến thức nâng cao hơn.
Hình chóp là hình đa diện được tạo thành bởi một mặt đáy là một đa giác và các mặt bên là các tam giác có chung đỉnh. Đỉnh chung đó gọi là đỉnh của hình chóp, các cạnh nối đỉnh với các đỉnh của đa giác đáy gọi là cạnh bên, và đa giác đáy gọi là mặt đáy.
Hình chóp tam giác đều là hình chóp có đáy là tam giác đều và các mặt bên là các tam giác cân bằng nhau. Trong hình chóp tam giác đều, đường cao đi qua tâm của tam giác đáy.
Hình chóp tứ giác đều là hình chóp có đáy là hình vuông và các mặt bên là các tam giác cân bằng nhau. Trong hình chóp tứ giác đều, đường cao đi qua tâm của hình vuông đáy.
Diện tích xung quanh của hình chóp đều được tính bằng công thức:
Sxq = p * d
Trong đó:
Diện tích toàn phần của hình chóp đều được tính bằng công thức:
Stp = Sxq + Sđáy
Trong đó:
Thể tích của hình chóp được tính bằng công thức:
V = (1/3) * Sđáy * h
Trong đó:
Ví dụ 1: Tính diện tích xung quanh của hình chóp tam giác đều có cạnh đáy là 5cm và trung đoạn là 4cm.
Giải:
Nửa chu vi đáy là: p = (5 + 5 + 5) / 2 = 7.5cm
Diện tích xung quanh là: Sxq = 7.5 * 4 = 30cm2
Ví dụ 2: Tính thể tích của hình chóp tứ giác đều có cạnh đáy là 6cm và chiều cao là 8cm.
Giải:
Diện tích đáy là: Sđáy = 6 * 6 = 36cm2
Thể tích của hình chóp là: V = (1/3) * 36 * 8 = 96cm3
Khi giải các bài toán về hình chóp, cần chú ý đến việc xác định đúng các yếu tố của hình chóp, áp dụng đúng công thức tính diện tích và thể tích. Việc vẽ hình minh họa sẽ giúp bạn hình dung rõ hơn về bài toán và tìm ra lời giải chính xác.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết Hình chóp tam giác đều – hình chóp tứ giác đều SGK Toán 8 - Chân trời sáng tạo. Chúc bạn học tập tốt!