Chào mừng các em học sinh đến với lời giải chi tiết Bài 10 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 8.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho hàm số
Đề bài
Cho hàm số \(y = f\left( x \right) = \dfrac{5}{{4x}}\).
a) Tính \(f\left( {\dfrac{1}{5}} \right);f\left( { - 5} \right);f\left( {\dfrac{4}{5}} \right)\).
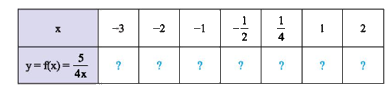
b) Hãy tìm các giá trị tương ứng của hàm số trong bảng sau:
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Giá trị của hàm số tại một điểm \(x = a\) là \(f\left( a \right)\).
Lời giải chi tiết
a) Ta có:
\(f\left( {\dfrac{1}{5}} \right) = \dfrac{5}{{4.\dfrac{1}{5}}} = \dfrac{5}{{\dfrac{4}{5}}} = 5:\dfrac{4}{5} = 5.\dfrac{5}{4} = \dfrac{{25}}{4};\)
\(f\left( { - 5} \right) = \dfrac{5}{{4.\left( { - 5} \right)}} = \dfrac{5}{{ - 20}} = \dfrac{{ - 1}}{4};\)
\(f\left( {\dfrac{4}{5}} \right) = \dfrac{5}{{4.\dfrac{4}{5}}} = \dfrac{5}{{\dfrac{{16}}{5}}} = 5:\dfrac{{16}}{5} = 5.\dfrac{5}{{16}} = \dfrac{{25}}{{16}}\)
b) Ta có:
\(f\left( { - 3} \right) = \dfrac{5}{{4.\left( { - 3} \right)}} = \dfrac{5}{{ - 12}} = \dfrac{{ - 5}}{{12}};\)
\(f\left( { - 2} \right) = \dfrac{5}{{4.\left( { - 2} \right)}} = \dfrac{5}{{ - 8}} = \dfrac{{ - 5}}{8};\)
\(f\left( { - 1} \right) = \dfrac{5}{{4.\left( { - 1} \right)}} = \dfrac{5}{{ - 4}} = \dfrac{{ - 5}}{4};\)
\(f\left( { - \dfrac{1}{2}} \right) = \dfrac{5}{{4.\left( { - \dfrac{1}{2}} \right)}} = \dfrac{5}{{\dfrac{{ - 4}}{2}}} = \dfrac{5}{{ - 2}} = \dfrac{{ - 5}}{2}\);
\(f\left( {\dfrac{1}{4}} \right) = \dfrac{5}{{4.\dfrac{1}{4}}} = \dfrac{5}{{\dfrac{4}{4}}} = \dfrac{5}{1} = 5\);
\(f\left( 1 \right) = \dfrac{5}{{4.1}} = \dfrac{5}{4}\);
\(f\left( 2 \right) = \dfrac{5}{{4.2}} = \dfrac{5}{8}\)
Ta có bảng sau:
\(x\) | –3 | –2 | –1 | \( - \dfrac{1}{2}\) | \(\dfrac{1}{4}\) | 1 | 2 |
\(y = f\left( x \right) = \dfrac{5}{{4x}}\) | \(\dfrac{{ - 5}}{{12}}\) | \(\dfrac{{ - 5}}{8}\) | \(\dfrac{{ - 5}}{4}\) | \(\dfrac{{ - 5}}{2}\) | 5 | \(\dfrac{5}{4}\) | \(\dfrac{5}{8}\) |
Bài 10 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức đã học về hình hộp chữ nhật và hình lập phương để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của các hình này.
Bài 10 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để tính diện tích xung quanh của hình hộp chữ nhật, ta sử dụng công thức: Diện tích xung quanh = 2 * (chiều dài + chiều rộng) * chiều cao. Trong bài toán này, cần xác định đúng chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật để áp dụng công thức một cách chính xác.
Diện tích toàn phần của hình hộp chữ nhật được tính bằng công thức: Diện tích toàn phần = Diện tích xung quanh + 2 * Diện tích đáy. Việc tính toán diện tích đáy (chiều dài * chiều rộng) là bước quan trọng để có được kết quả chính xác.
Thể tích của hình hộp chữ nhật được tính bằng công thức: Thể tích = chiều dài * chiều rộng * chiều cao. Đối với hình lập phương, thể tích được tính bằng công thức: Thể tích = cạnh * cạnh * cạnh. Đảm bảo sử dụng đúng đơn vị đo để có kết quả chính xác.
Giả sử một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Hãy tính:
Giải:
Để giải nhanh các bài toán về hình hộp chữ nhật và hình lập phương, hãy:
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập tương tự trong SGK và sách bài tập Toán 8 tập 2. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Bài 10 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp các em hiểu rõ hơn về hình hộp chữ nhật và hình lập phương. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.
| Công thức | Mô tả |
|---|---|
| Diện tích xung quanh (Hộp chữ nhật) | 2 * (dài + rộng) * cao |
| Diện tích toàn phần (Hộp chữ nhật) | Diện tích xung quanh + 2 * (dài * rộng) |
| Thể tích (Hộp chữ nhật) | dài * rộng * cao |
| Thể tích (Hình lập phương) | cạnh * cạnh * cạnh |