Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 44, 45 SGK Toán 8 tập 2 – Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập này thuộc chương trình Toán 8 tập 2, tập trung vào việc rèn luyện kỹ năng giải toán và áp dụng các kiến thức đã học vào thực tế.
a) Cho hai số 5 và 8. Hãy tính tỉ số giữa hai số đã cho.
Video hướng dẫn giải
Hãy tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) trong các trường hợp sau:
a) \(AB = 6cm;CD = 8cm\);
b) \(AB = 1,2m;CD = 42cm\).
Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
a) Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{6}{8} = \frac{3}{4}\).
b) Đổi \(1,2m = 120cm\)
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{{120}}{{42}} = \frac{{20}}{7}\).
Video hướng dẫn giải
a) Cho hai số 5 và 8. Hãy tính tỉ số giữa hai số đã cho.
b) Hãy đo và tính tỉ số giữa hai độ dài (theo mm) của hai đoạn thẳng \(AB\) và \(CD\) trong Hình 1.

Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
a) Tỉ số giữa hai số 5 và 8 là \(5:8 = \frac{5}{8}\).
b) Ta có: AB = 35mm; CD = 45mm
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{35}{45}=\frac{7}{9}\).
Video hướng dẫn giải
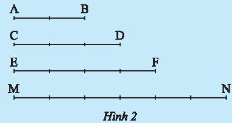
So sánh tỉ số của hai đoạn thẳng \(AB\) và \(CD\) với tỉ số của hai đoạn thẳng \(EF\) và \(MN\) trong Hình 2.
Phương pháp giải:
Ta tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) ; tỉ số của hai đoạn thẳng \(EF\) và \(MN\) sau đó so sánh.
Lời giải chi tiết:
Ta coi mỗi vạch chia là 1 đơn vị. Do đó, độ dài các đoạn thẳng là \(AB = 2\) đơn vị; \(CD = 3\) đơn vị; \(EF = 4\) đơn vị; \(MN = 6\) đơn vị.
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{2}{3}\).
Tỉ số giữa hai đoạn thẳng \(EF\) và \(MN\) là \(EF:MN = \frac{{EF}}{{MN}} = \frac{4}{6} = \frac{2}{3}\).
Do đó, tỉ số của hai đoạn thẳng \(AB\) và \(CD\) bằng tỉ số của hai đoạn thẳng \(EF\) và \(MN\) .
Video hướng dẫn giải
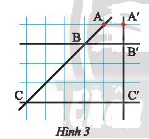
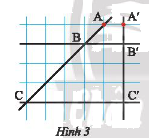
Trong Hình 3, chứng minh rằng:
a) \(AB\) và \(BC\) tỉ lệ với \(A'B'\) và \(B'C'\);
b) \(AC\) và \(A'C'\) tỉ lệ với \(AB\) và \(A'B'\).
Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
Ta xem độ dài một cạnh của hình vuông nhỏ là \(a\) và đường chéo của một hình vuông nhỏ là \(b\).
Khi đó, độ dài các đoạn thẳng là
\(AB = b;BC = 3b;A'B' = a;B'C' = 3a;AC = 4b;A'C' = 4a\)
a) Tỉ số của \(AB\) và \(BC\)là \(\frac{{AB}}{{BC}} = \frac{b}{{3b}} = \frac{1}{3}\).
Tỉ số của \(A'B'\) và \(B'C'\) là \(\frac{{A'B'}}{{B'C'}} = \frac{a}{{3a}} = \frac{1}{3}\).
Do đó, \(AB\) và \(BC\) tỉ lệ với \(A'B'\) và \(B'C'\).
b) Tỉ số của \(AC\) và \(A'C'\)là \(\frac{{AC}}{{A'C'}} = \frac{{4b}}{{4a}} = \frac{b}{a}\).
Tỉ số của \(AB\) và \(A'B'\) là \(\frac{{AB}}{{A'B'}} = \frac{b}{a}\).
Do đó, \(AC\) và \(A'C'\) tỉ lệ với \(AB\) và \(A'B'\).
Video hướng dẫn giải
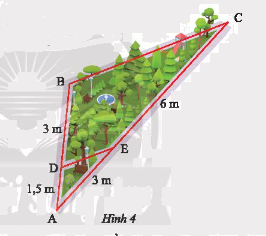
Hãy tìm các đoạn thẳng tỉ lệ trong hình vẽ sơ đồ một góc công viên ở Hình 4.
Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
Ta có:
\(AD = 1,5m;AE = 3m;BD = 3m;EC = 6m;\)
\(AB = AD + DB = 1,5 + 3 = 4,5m;AC = AE + EC = 3 + 6 = 9m\)
Ta có:
\(\frac{{AD}}{{BD}} = \frac{{1,5}}{3} = \frac{1}{2};\frac{{AE}}{{EC}} = \frac{3}{6} = \frac{1}{2}\). Do đó, \(AD\) và \(BD\) tỉ lệ với \(AE\) và \(EC\).
\(\frac{{AD}}{{AB}} = \frac{{1,5}}{{4,5}} = \frac{1}{3};\frac{{AE}}{{AC}} = \frac{3}{9} = \frac{1}{3}\). Do đó, \(AD\) và \(AB\) tỉ lệ với \(AE\) và \(AC\).
\(\frac{{AB}}{{BD}} = \frac{{4,5}}{3} = \frac{3}{2};\frac{{AC}}{{EC}} = \frac{9}{6} = \frac{3}{2}\). Do đó, \(AB\) và \(BD\) tỉ lệ với \(AC\) và \(EC\).
Video hướng dẫn giải
a) Cho hai số 5 và 8. Hãy tính tỉ số giữa hai số đã cho.
b) Hãy đo và tính tỉ số giữa hai độ dài (theo mm) của hai đoạn thẳng \(AB\) và \(CD\) trong Hình 1.

Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
a) Tỉ số giữa hai số 5 và 8 là \(5:8 = \frac{5}{8}\).
b) Ta có: AB = 35mm; CD = 45mm
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{35}{45}=\frac{7}{9}\).
Video hướng dẫn giải
Hãy tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) trong các trường hợp sau:
a) \(AB = 6cm;CD = 8cm\);
b) \(AB = 1,2m;CD = 42cm\).
Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
a) Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{6}{8} = \frac{3}{4}\).
b) Đổi \(1,2m = 120cm\)
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{{120}}{{42}} = \frac{{20}}{7}\).
Video hướng dẫn giải
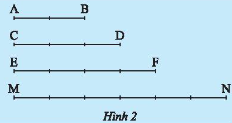
So sánh tỉ số của hai đoạn thẳng \(AB\) và \(CD\) với tỉ số của hai đoạn thẳng \(EF\) và \(MN\) trong Hình 2.
Phương pháp giải:
Ta tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) ; tỉ số của hai đoạn thẳng \(EF\) và \(MN\) sau đó so sánh.
Lời giải chi tiết:
Ta coi mỗi vạch chia là 1 đơn vị. Do đó, độ dài các đoạn thẳng là \(AB = 2\) đơn vị; \(CD = 3\) đơn vị; \(EF = 4\) đơn vị; \(MN = 6\) đơn vị.
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{2}{3}\).
Tỉ số giữa hai đoạn thẳng \(EF\) và \(MN\) là \(EF:MN = \frac{{EF}}{{MN}} = \frac{4}{6} = \frac{2}{3}\).
Do đó, tỉ số của hai đoạn thẳng \(AB\) và \(CD\) bằng tỉ số của hai đoạn thẳng \(EF\) và \(MN\) .
Video hướng dẫn giải
Trong Hình 3, chứng minh rằng:
a) \(AB\) và \(BC\) tỉ lệ với \(A'B'\) và \(B'C'\);
b) \(AC\) và \(A'C'\) tỉ lệ với \(AB\) và \(A'B'\).
Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
Ta xem độ dài một cạnh của hình vuông nhỏ là \(a\) và đường chéo của một hình vuông nhỏ là \(b\).
Khi đó, độ dài các đoạn thẳng là
\(AB = b;BC = 3b;A'B' = a;B'C' = 3a;AC = 4b;A'C' = 4a\)
a) Tỉ số của \(AB\) và \(BC\)là \(\frac{{AB}}{{BC}} = \frac{b}{{3b}} = \frac{1}{3}\).
Tỉ số của \(A'B'\) và \(B'C'\) là \(\frac{{A'B'}}{{B'C'}} = \frac{a}{{3a}} = \frac{1}{3}\).
Do đó, \(AB\) và \(BC\) tỉ lệ với \(A'B'\) và \(B'C'\).
b) Tỉ số của \(AC\) và \(A'C'\)là \(\frac{{AC}}{{A'C'}} = \frac{{4b}}{{4a}} = \frac{b}{a}\).
Tỉ số của \(AB\) và \(A'B'\) là \(\frac{{AB}}{{A'B'}} = \frac{b}{a}\).
Do đó, \(AC\) và \(A'C'\) tỉ lệ với \(AB\) và \(A'B'\).
Video hướng dẫn giải
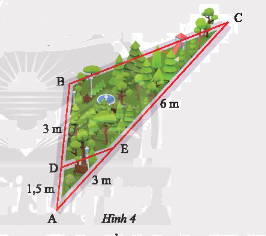
Hãy tìm các đoạn thẳng tỉ lệ trong hình vẽ sơ đồ một góc công viên ở Hình 4.
Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
Ta có:
\(AD = 1,5m;AE = 3m;BD = 3m;EC = 6m;\)
\(AB = AD + DB = 1,5 + 3 = 4,5m;AC = AE + EC = 3 + 6 = 9m\)
Ta có:
\(\frac{{AD}}{{BD}} = \frac{{1,5}}{3} = \frac{1}{2};\frac{{AE}}{{EC}} = \frac{3}{6} = \frac{1}{2}\). Do đó, \(AD\) và \(BD\) tỉ lệ với \(AE\) và \(EC\).
\(\frac{{AD}}{{AB}} = \frac{{1,5}}{{4,5}} = \frac{1}{3};\frac{{AE}}{{AC}} = \frac{3}{9} = \frac{1}{3}\). Do đó, \(AD\) và \(AB\) tỉ lệ với \(AE\) và \(AC\).
\(\frac{{AB}}{{BD}} = \frac{{4,5}}{3} = \frac{3}{2};\frac{{AC}}{{EC}} = \frac{9}{6} = \frac{3}{2}\). Do đó, \(AB\) và \(BD\) tỉ lệ với \(AC\) và \(EC\).
Mục 1 trang 44, 45 SGK Toán 8 tập 2 – Chân trời sáng tạo là một phần quan trọng trong chương trình học, tập trung vào việc củng cố kiến thức về các phép biến đổi đại số và ứng dụng vào giải toán. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc biến đổi.
Mục 1 thường bao gồm các bài tập về:
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 1 trang 44, 45 SGK Toán 8 tập 2 – Chân trời sáng tạo:
Ví dụ: Phân tích đa thức x2 - 4x + 4 thành nhân tử.
Lời giải:
x2 - 4x + 4 = (x - 2)2
Ví dụ: Rút gọn biểu thức (2x + 3)(x - 1) - (x + 2)2
Lời giải:
(2x + 3)(x - 1) - (x + 2)2 = 2x2 - 2x + 3x - 3 - (x2 + 4x + 4) = 2x2 + x - 3 - x2 - 4x - 4 = x2 - 3x - 7
Ví dụ: Giải phương trình 3x - 5 = 7
Lời giải:
3x - 5 = 7 => 3x = 12 => x = 4
Để giải các bài tập trong Mục 1 một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
ax = b và giải để tìm ra giá trị của x.Khi giải bài tập, học sinh cần lưu ý:
Kiến thức về phân tích đa thức, rút gọn biểu thức và giải phương trình bậc nhất một ẩn có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và thực tế, như giải các bài toán hình học, vật lý, kinh tế,...
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải các bài tập trong Mục 1 trang 44, 45 SGK Toán 8 tập 2 – Chân trời sáng tạo. Chúc các em học tập tốt!