Bài 10 trang 117 SGK Toán 8 tập 1 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các phép biến đổi đồng dạng để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 117 SGK Toán 8 tập 1 – Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
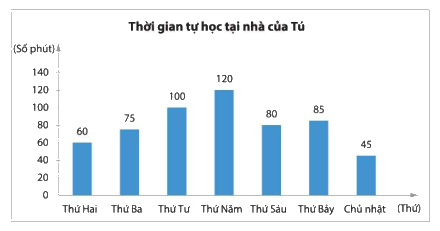
Thời gian tự học tại nhà của bạn Tú
Đề bài
Thời gian tự học tại nhà của bạn Tú trong một tuần được biểu diễn trong biểu đồ cột sau đây. Em hãy vẽ biểu đồ đoạn thẳng tương ứng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng vẽ biểu đồ đoạn thẳng
Lời giải chi tiết
Ta có:
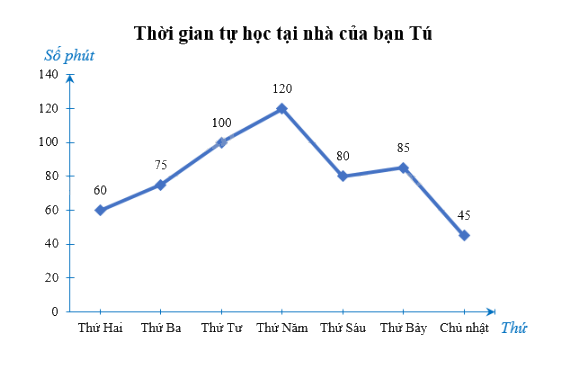
Thứ | Thứ Hai | Thứ Ba | Thứ Tư | Thứ Năm | Thứ Sáu | Thứ Bảy | Chủ nhật |
Thời gian tự học tại nhà của Tú (phút) | 60 | 75 | 100 | 120 | 80 | 85 | 45 |
Biểu đồ đoạn thẳng biểu diễn thời gian tự học tại nhà của bạn Tú trong một tuần:
Bài 10 trang 117 SGK Toán 8 tập 1 – Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng kiến thức về các phép biến đổi đồng dạng để giải quyết các bài toán liên quan đến hình học. Để giúp học sinh hiểu rõ hơn về bài tập này, giaitoan.edu.vn xin trình bày lời giải chi tiết và dễ hiểu nhất.
(Nội dung đề bài sẽ được chèn vào đây. Ví dụ: Cho hình vuông ABCD có cạnh bằng a. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng MNPQ là một hình vuông.)
Để giải bài toán này, chúng ta cần hiểu rõ các khái niệm về phép biến đổi đồng dạng, đặc biệt là phép tịnh tiến, phép quay và phép vị tự. Đồng thời, cần nắm vững các tính chất của hình vuông để chứng minh MNPQ cũng là một hình vuông.
Bước 1: Xác định các yếu tố cần thiết
Bước 2: Chứng minh MNPQ là hình vuông
Để chứng minh MNPQ là hình vuông, chúng ta cần chứng minh:
(Tiếp tục trình bày chi tiết các bước chứng minh, sử dụng các định lý và tính chất hình học đã học. Ví dụ: Sử dụng định lý Pitago để tính độ dài các cạnh MNPQ, sử dụng tính chất của trung điểm để chứng minh các cạnh đối song song và bằng nhau, sử dụng tính chất của góc vuông để chứng minh MNPQ có bốn góc vuông.)
Qua các bước chứng minh trên, ta có thể kết luận rằng MNPQ là một hình vuông.
Để hiểu sâu hơn về bài toán này, các em có thể thử giải các bài tập tương tự với các hình dạng khác nhau. Ví dụ:
Khi giải các bài tập về phép biến đổi đồng dạng, các em cần lưu ý:
Để học tốt môn Toán 8, các em có thể tham khảo các tài liệu sau:
Hy vọng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập về phép biến đổi đồng dạng. Chúc các em học tốt!