Chào mừng các em học sinh đến với lời giải chi tiết bài 12 trang 59 SGK Toán 8 tập 2 – Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án, cách giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về bài học.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học toán một cách hiệu quả và dễ dàng.
Cho tam giác
Đề bài
Cho tam giác \(ABC\) có \(BC\) bằng 30cm. Trên đường cao \(AH\) lấy các điểm \(K,I\) sao cho \(AK = KI = IH\). Qua \(I\) và \(K\) vẽ các đường \(EF//BC,MN//BC\left( {E,M \in AB;F,N \in AC} \right)\).
a) Tính độ dài các đoạn thẳng \(MN\) và \(EF\).
b) Tính diện tích tứ giác \(MNFE\) biết rằng diện tích tam giác \(ABC\) là \(10,8d{m^2}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết
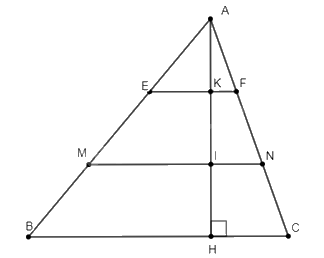
a) Vì \(AK = KI = IH \Rightarrow AK = \frac{1}{3}AH;AI = \frac{2}{3}AH\).
Vì \(EF//BC \Rightarrow EK//BH;MN//BC \Rightarrow MI//BH\)
Xét tam giác \(ABH\) ta có \(EK//BH\), theo định lí Thales ta có:
\(\frac{{AE}}{{AB}} = \frac{{AK}}{{AH}} = \frac{1}{3}\)
Xét tam giác \(ABH\) ta có \(MI//BH\), theo định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{AI}}{{AH}} = \frac{2}{3}\)
Xét tam giác \(ABC\) ta có \(EF//BC\), theo hệ quả của định lí Thales ta có:
\(\frac{{AE}}{{AB}} = \frac{{EF}}{{BC}} = \frac{1}{3} \Rightarrow \frac{{EF}}{{30}} = \frac{1}{3} \Rightarrow EF = \frac{{30.1}}{3} = 10\)
Xét tam giác \(ABC\) ta có \(MN//BC\), theo hệ quả của định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{MN}}{{BC}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{30}} = \frac{2}{3} \Rightarrow MN = \frac{{30.2}}{3} = 20\)
Vậy \(EF = 10cm;MN = 20cm\).
b) Đổi \(10,8d{m^2} = 1080c{m^2}\)
Diện tích tam giác \(ABC\) là:
\({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}AH.30 = 1080\left( {c{m^2}} \right)\)
\( \Rightarrow AH = 1080.2:30 = 72cm\)
Ta có: \(AH \bot BC \Rightarrow AH \bot MN\) (quan hệ từ vuông góc đến song song)
Do đó, \(KI \bot MN\)
Mà \(KI = \frac{1}{3}AH \Rightarrow KI = \frac{1}{3}.72 = 24cm\)
Tứ giác \(MNFE\) có \(MN//EF\) (cùng song song với \(BC\)) nên tứ giác \(MNFE\) là hình thang.
Lại có: \(KI \bot MN \Rightarrow KI\)là đường cao của hình thang.
Diện tích hình thang \(MNFE\) là:
\({S_{MNFE}} = \frac{1}{2}\left( {EF + MN} \right).KI = \frac{1}{2}.\left( {10 + 20} \right).24 = 360\left( {c{m^2}} \right)\)
Vậy diện tích tứ giác \(MNFE\) là \(360c{m^2}\).
Bài 12 trang 59 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình đại số lớp 8, tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đại số đơn giản. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 12 trang 59 SGK Toán 8 tập 2 – Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng bài tập:
Ví dụ: Tính giá trị của biểu thức 3x + 2y khi x = 2 và y = -1.
Lời giải:
Thay x = 2 và y = -1 vào biểu thức, ta được:
3x + 2y = 3(2) + 2(-1) = 6 - 2 = 4
Vậy, giá trị của biểu thức 3x + 2y khi x = 2 và y = -1 là 4.
Ví dụ: Rút gọn biểu thức 2x + 3x - 5x.
Lời giải:
2x + 3x - 5x = (2 + 3 - 5)x = 0x = 0
Vậy, biểu thức 2x + 3x - 5x được rút gọn thành 0.
Ví dụ: Tìm x biết 2x + 5 = 11.
Lời giải:
2x + 5 = 11
2x = 11 - 5
2x = 6
x = 6 / 2
x = 3
Vậy, x = 3.
Ví dụ: Một cửa hàng bán được 15 cái áo với giá 80.000 đồng/cái và 10 cái quần với giá 120.000 đồng/cái. Hỏi cửa hàng thu được bao nhiêu tiền?
Lời giải:
Số tiền thu được từ bán áo là: 15 x 80.000 = 1.200.000 đồng
Số tiền thu được từ bán quần là: 10 x 120.000 = 1.200.000 đồng
Tổng số tiền cửa hàng thu được là: 1.200.000 + 1.200.000 = 2.400.000 đồng
Vậy, cửa hàng thu được 2.400.000 đồng.
Để giải bài tập về các phép biến đổi đại số đơn giản một cách hiệu quả, các em nên:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em đã hiểu rõ hơn về cách giải bài 12 trang 59 SGK Toán 8 tập 2 – Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!