Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 73, 74 SGK Toán 8 tập 2 – Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải bài tập.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho các em những lời giải chính xác và đầy đủ nhất.
a) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác
Video hướng dẫn giải
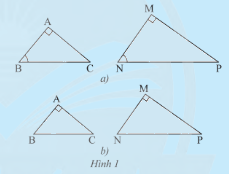
a) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác \(ABC\) vuông tại \(A\) và tam giác \(MNP\) vuông tại \(M\) có \(\widehat B = \widehat N\) thì hai tam giác đó có đồng dạng với nhau không.
b) Từ trường hợp đồng dạng thứ hai của hai tam giác, xét xem nếu tam giác \(ABC\) vuông tại \(A\) và tam giác \(MNP\) vuông tại \(M\) có \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) thì hai tam giác đó có đồng dạng với nhau không.
Phương pháp giải:
- Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau.
- Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
a) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\widehat B = \widehat N\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (g.g)
b) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (c.g.c).
Video hướng dẫn giải
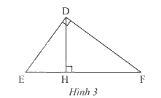
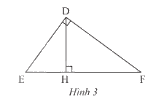
Cho tam giác \(DEF\) vuông tại \(D\) có \(DH\) là đường cao (Hình 3). Chứng minh rằng \(D{E^2} = EH.EF\)
Phương pháp giải:
Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải chi tiết:
Vì \(DH \bot EF \Rightarrow \widehat {DHE} = 90^\circ \)
Xét tam giác \(DEH\) và tam giác \(FED\) ta có:
\(\widehat E\) chung
\(\widehat {DHE} = \widehat {EDF} = 90^\circ \).
Do đó, \(\Delta DEH\backsim\Delta FED\) (g.g)
Suy ra, \(\frac{{DE}}{{EF}} = \frac{{EH}}{{DE}} \Rightarrow D{E^2} = EF.EH\) (điều phải chứng minh).
Video hướng dẫn giải
Tính chiều cao của cột cờ trong hoạt động khởi động trang 73.
Phương pháp giải:
Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải chi tiết:
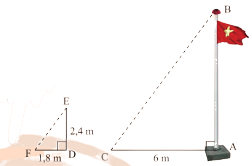
Cùng một thời điểm thì góc tạo bởi tia nắng và mặt đất là như nhau. Do đó, \(\widehat {EFD} = \widehat {BCA}\).
Xét tam giác \(DEF\) và tam giác \(ABC\) ta có:
\(\widehat {EFD} = \widehat {BCA}\) (chứng minh trên)
\(\widehat {EDF} = \widehat {BAC} = 90^\circ \).
Do đó, \(\Delta DEF\backsim\Delta ABC\) (g.g)
Suy ra, \(\frac{{FD}}{{AC}} = \frac{{ED}}{{AB}} \Leftrightarrow \frac{{1,8}}{6} = \frac{{2,4}}{{AB}} \Rightarrow AB = \frac{{6.2,4}}{{1,8}} = 8\).
Vậy cột cờ \(AB\) cao 8m.
Video hướng dẫn giải
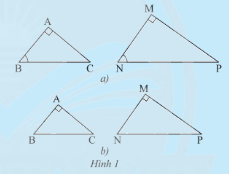
a) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác \(ABC\) vuông tại \(A\) và tam giác \(MNP\) vuông tại \(M\) có \(\widehat B = \widehat N\) thì hai tam giác đó có đồng dạng với nhau không.
b) Từ trường hợp đồng dạng thứ hai của hai tam giác, xét xem nếu tam giác \(ABC\) vuông tại \(A\) và tam giác \(MNP\) vuông tại \(M\) có \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) thì hai tam giác đó có đồng dạng với nhau không.
Phương pháp giải:
- Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau.
- Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
a) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\widehat B = \widehat N\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (g.g)
b) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (c.g.c).
Video hướng dẫn giải
Cho tam giác \(DEF\) vuông tại \(D\) có \(DH\) là đường cao (Hình 3). Chứng minh rằng \(D{E^2} = EH.EF\)
Phương pháp giải:
Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải chi tiết:
Vì \(DH \bot EF \Rightarrow \widehat {DHE} = 90^\circ \)
Xét tam giác \(DEH\) và tam giác \(FED\) ta có:
\(\widehat E\) chung
\(\widehat {DHE} = \widehat {EDF} = 90^\circ \).
Do đó, \(\Delta DEH\backsim\Delta FED\) (g.g)
Suy ra, \(\frac{{DE}}{{EF}} = \frac{{EH}}{{DE}} \Rightarrow D{E^2} = EF.EH\) (điều phải chứng minh).
Video hướng dẫn giải
Tính chiều cao của cột cờ trong hoạt động khởi động trang 73.
Phương pháp giải:
Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải chi tiết:
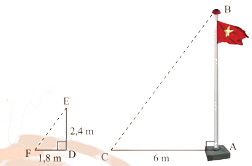
Cùng một thời điểm thì góc tạo bởi tia nắng và mặt đất là như nhau. Do đó, \(\widehat {EFD} = \widehat {BCA}\).
Xét tam giác \(DEF\) và tam giác \(ABC\) ta có:
\(\widehat {EFD} = \widehat {BCA}\) (chứng minh trên)
\(\widehat {EDF} = \widehat {BAC} = 90^\circ \).
Do đó, \(\Delta DEF\backsim\Delta ABC\) (g.g)
Suy ra, \(\frac{{FD}}{{AC}} = \frac{{ED}}{{AB}} \Leftrightarrow \frac{{1,8}}{6} = \frac{{2,4}}{{AB}} \Rightarrow AB = \frac{{6.2,4}}{{1,8}} = 8\).
Vậy cột cờ \(AB\) cao 8m.
Mục 1 của chương trình Toán 8 tập 2 – Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa các kiến thức về tứ giác. Các bài tập trong mục này yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng và rèn luyện kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong các bài kiểm tra và thi cử.
Bài tập mục 1 trang 73, 74 SGK Toán 8 tập 2 – Chân trời sáng tạo bao gồm các dạng bài tập sau:
Bài 1 yêu cầu học sinh xác định các yếu tố của tứ giác ABCD. Để giải bài này, học sinh cần vận dụng các định nghĩa và tính chất của tứ giác để xác định các góc, cạnh, đường chéo của tứ giác. Ví dụ, nếu tứ giác ABCD là hình bình hành thì các cạnh đối song song và bằng nhau, các góc đối bằng nhau.
Bài 2 yêu cầu học sinh chứng minh một tứ giác là hình bình hành. Để giải bài này, học sinh cần chứng minh một trong các điều kiện sau:
Ví dụ, để chứng minh tứ giác ABCD là hình bình hành, ta có thể chứng minh AB song song CD và AD song song BC.
Bài 3 yêu cầu học sinh tính độ dài các cạnh, đường chéo của tứ giác. Để giải bài này, học sinh cần vận dụng các định lý và tính chất của tứ giác, cũng như các kiến thức về tam giác (định lý Pitago, hệ thức lượng trong tam giác vuông). Ví dụ, nếu tứ giác ABCD là hình chữ nhật thì các góc đều bằng 90 độ và đường chéo bằng nhau.
Để giải tốt các bài tập về tứ giác, học sinh cần lưu ý những điều sau:
Kiến thức về tứ giác có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, thiết kế đồ họa. Ví dụ, các hình chữ nhật, hình vuông được sử dụng rộng rãi trong việc thiết kế các công trình xây dựng, các đồ vật trong gia đình. Các hình bình hành, hình thoi được sử dụng trong việc thiết kế các họa tiết trang trí.
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập mục 1 trang 73, 74 SGK Toán 8 tập 2 – Chân trời sáng tạo, các em học sinh sẽ hiểu rõ hơn về kiến thức về tứ giác và tự tin giải các bài tập liên quan. Chúc các em học tập tốt!