Chào mừng bạn đến với bài học về lý thuyết các trường hợp đồng dạng của hai tam giác trong chương trình Toán 8 - Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về chủ đề này.
Chúng ta sẽ cùng nhau tìm hiểu các định nghĩa, tính chất và đặc biệt là các trường hợp để nhận biết hai tam giác đồng dạng. Việc nắm vững lý thuyết này là nền tảng để giải quyết các bài tập liên quan một cách hiệu quả.
Có những trường hợp đồng dạng nào của hai tam giác?
1. Trường hợp đồng dạng thứ nhất (Cạnh – cạnh – cạnh)
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
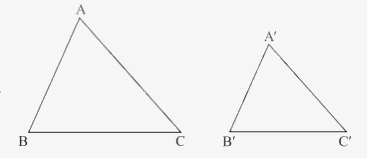
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\,(c.c.c)\end{array}\)
Nhận xét: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số chu vi của hai tam giác đó cũng bằng k.
2. Trường hợp đồng dạng thứ hai (cạnh – góc – cạnh)
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
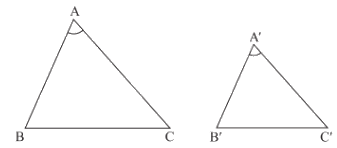
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}},\widehat {A'} = \widehat A\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\,(c.g.c)\end{array}\)
Nhận xét: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số hai đường trung tuyến tương ứng của hai tam giác đó cũng bằng k.
3. Trường hợp đồng dạng thứ ba (góc – góc)
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
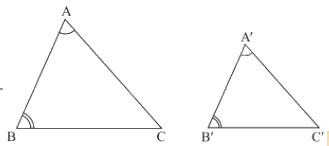
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\widehat {A'} = \widehat A,\widehat {B'} = \widehat B\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\end{array}\)
Nhận xét: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số hai đường phân giác tương ứng của hai tam giác đó cũng bằng k.
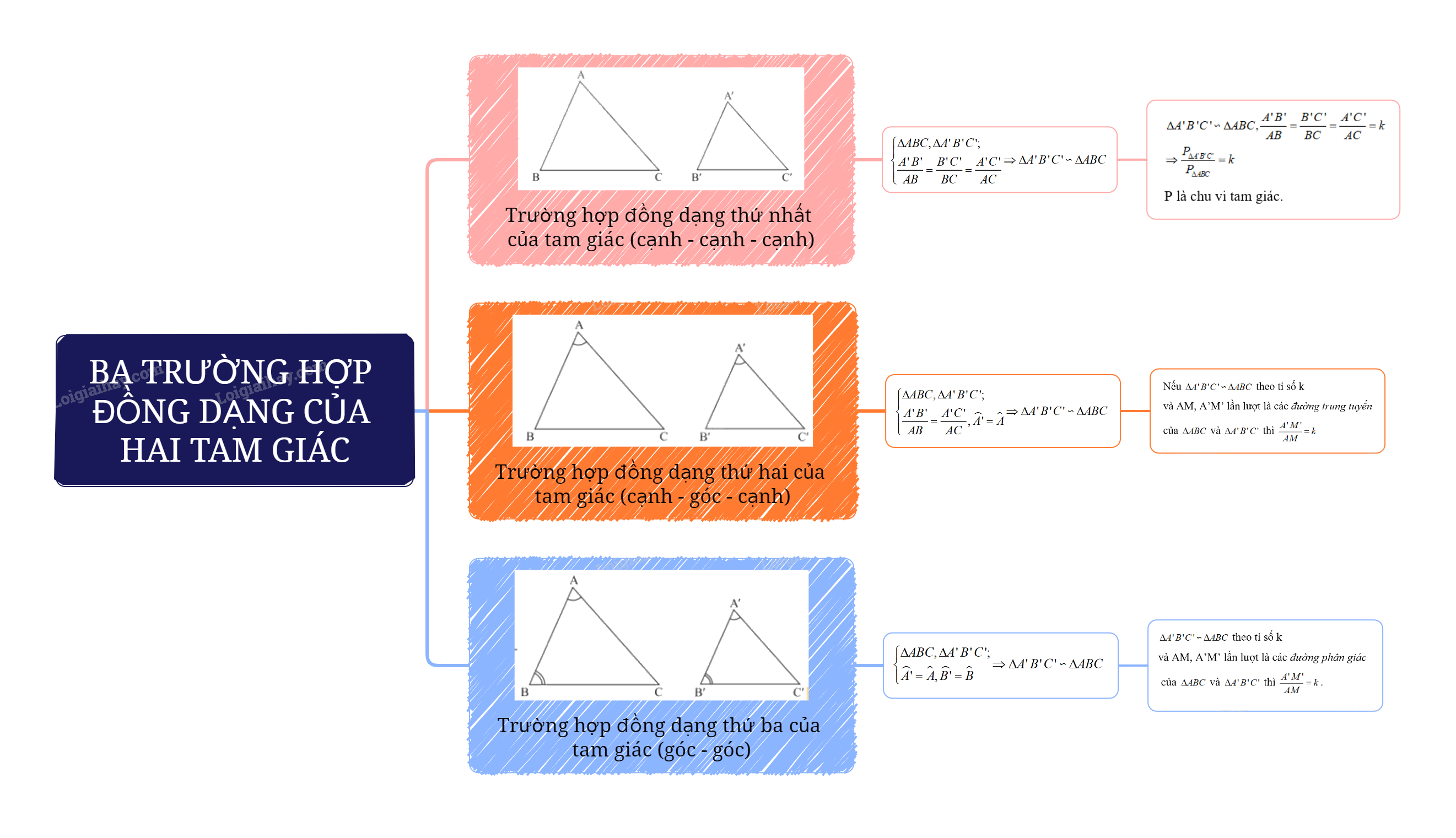
Trong chương trình Toán 8, chủ đề về tam giác đồng dạng đóng vai trò quan trọng, giúp học sinh hiểu rõ hơn về mối quan hệ giữa các hình và ứng dụng trong thực tế. Bài viết này sẽ trình bày chi tiết lý thuyết về các trường hợp đồng dạng của hai tam giác theo sách giáo khoa Toán 8 - Chân trời sáng tạo.
Hai tam giác được gọi là đồng dạng với nhau nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Kí hiệu: ΔABC ~ ΔA'B'C'
Điều kiện cần và đủ để ΔABC ~ ΔA'B'C' là:
Có ba trường hợp đồng dạng của hai tam giác thường được sử dụng:
ΔABC ~ ΔA'B'C' nếu ∠A = ∠A' và ∠B = ∠B' (hoặc ∠A = ∠A' và ∠C = ∠C', hoặc ∠B = ∠B' và ∠C = ∠C').
ΔABC ~ ΔA'B'C' nếu AB/A'B' = AC/A'C' và ∠A = ∠A'.
ΔABC ~ ΔA'B'C' nếu AB/A'B' = BC/B'C' = CA/C'A'.
Các trường hợp đồng dạng được sử dụng để:
Ví dụ 1: Cho ΔABC và ΔA'B'C' có ∠A = ∠A' = 60°, ∠B = ∠B' = 80°. Chứng minh ΔABC ~ ΔA'B'C'.
Giải: Vì ∠A = ∠A' và ∠B = ∠B' nên theo trường hợp 1, ΔABC ~ ΔA'B'C'.
Ví dụ 2: Cho ΔABC có AB = 3cm, AC = 4cm, ∠A = 90°. Cho ΔA'B'C' có A'B' = 6cm, A'C' = 8cm, ∠A' = 90°. Chứng minh ΔABC ~ ΔA'B'C'.
Giải: Ta có AB/A'B' = 3/6 = 1/2 và AC/A'C' = 4/8 = 1/2. Suy ra AB/A'B' = AC/A'C'. Vì ∠A = ∠A' = 90° nên theo trường hợp 2, ΔABC ~ ΔA'B'C'.
Để củng cố kiến thức về các trường hợp đồng dạng của hai tam giác, bạn có thể thực hành các bài tập sau:
Lý thuyết về các trường hợp đồng dạng của hai tam giác là một phần quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.