Bài 3 trang 57 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 57 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tam giác
Đề bài
Tam giác \(ABC\) có \(AB = 15cm,AC = 20cm,BC = 25cm\). Đường phân giác của góc \(BAC\)cắt \(BC\) tại \(D\). Qua \(D\) vẽ \(DE//AB\left( {E \in AC} \right)\).
a) Tính độ dài các đoạn thẳng \(BD,DC\) và \(DE\).
b) Chứng minh \(ABC\) là tam giác vuông. Tính diện tích tam giác \(ABC\).
c) Tính diện tích tam giác \(ADB,ADE\) và \(DCE\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Sử dụng Tính chất đường phân giác trong tam giác:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
- Diện tích tam giác
\(S = \frac{1}{2}a.h\) với \(a\) là độ dài đáy và \(h\) là chiều cao.
- Định lí Py – ta – go đảo
Nếu một tam giác có bình phương cạnh thứ nhất bằng tổng của bình phương cạnh thứ hai và cạnh thứ ba thì tam giác đó là tam giác vuông.
- Hệ quả của định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại của tam giác thì tạo ra một tam giác mới tỉ lệ với tam giác ban đầu.
Lời giải chi tiết
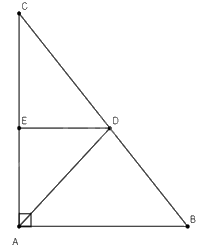
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
Bài 3 trang 57 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh thực hiện các phép tính đại số, thường liên quan đến việc thu gọn biểu thức, tìm giá trị của biểu thức, hoặc chứng minh đẳng thức. Để giải bài tập này hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Để giúp học sinh hiểu rõ hơn về cách giải bài 3 trang 57, chúng ta sẽ đi vào phân tích từng phần của bài tập. (Giả sử bài tập có nhiều phần, mỗi phần sẽ được giải thích chi tiết)
Đề bài: (Nêu lại đề bài phần a)
Lời giải:
Ví dụ:
(Giải chi tiết các bước biến đổi và tính toán)
Đề bài: (Nêu lại đề bài phần b)
Lời giải:
Ví dụ:
(Giải chi tiết các bước biến đổi và tính toán)
Để củng cố kiến thức về bài 3 trang 57, học sinh có thể tự giải các bài tập tương tự. Dưới đây là một số gợi ý:
Khi giải các bài tập đại số, học sinh cần lưu ý một số điều sau:
Các bài tập đại số không chỉ giúp học sinh rèn luyện kỹ năng tính toán mà còn có ứng dụng thực tế cao. Ví dụ, trong lĩnh vực kinh tế, đại số được sử dụng để xây dựng các mô hình tài chính, phân tích thị trường. Trong lĩnh vực khoa học tự nhiên, đại số được sử dụng để mô tả các hiện tượng vật lý, hóa học.
Bài 3 trang 57 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh nắm vững kiến thức về các phép biến đổi đại số. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và giải bài tập.