Bài 5 trang 62 SGK Toán 8 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào các tình huống khác.
Cho biết thang của một xe máy cứu hỏa có chiều dài (13)m,
Đề bài
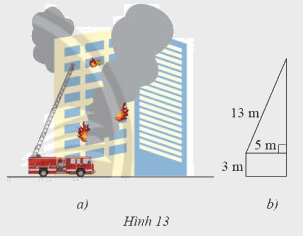
Cho biết thang của một xe máy cứu hỏa có chiều dài \(13\)m, chân thang cách mặt đất \(3\)m và cách tường của toàn nhà \(5\)m. Tính chiều cao mà thang có thể vươn tới.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định lý Pythagore tính khoảng cách của xe đến đầu thang
Tính chiều cao mà thang có thể vươn tới
Lời giải chi tiết
Gọi \(x\) là khoảng cách của xe đến đầu thang (m)
Áp dụng định lý Pythagore vào tam giác vuông trong hình ta có:
\({x^2} + {5^2} = {13^2}\)
\({x^2} = {13^2} - {5^2} = 144 = {12^2}\)
\(x = 12\) (m)
Chiều cao mà thang có thể vươn tới là:
\(12 + 3 = 15\) (m)
Bài 5 trang 62 SGK Toán 8 – Chân trời sáng tạo yêu cầu học sinh thực hiện các phép biến đổi đại số để rút gọn biểu thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về dấu ngoặc, quy tắc chuyển vế, và các phép toán cơ bản.
Bài tập này thường bao gồm các biểu thức chứa nhiều số hạng, các phép cộng, trừ, nhân, chia, và các dấu ngoặc. Mục tiêu là rút gọn biểu thức về dạng đơn giản nhất.
Giả sử bài tập yêu cầu rút gọn biểu thức: 2x + 3(x - 1) - 5x
Để tránh sai sót, học sinh cần:
Ngoài SGK Toán 8 Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
Giải bài 5 trang 62 SGK Toán 8 – Chân trời sáng tạo đòi hỏi học sinh phải nắm vững các quy tắc về phép biến đổi đại số và thực hành thường xuyên. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.