Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho từng bài tập trong SGK Toán 8 tập 1 – Chân trời sáng tạo, đặc biệt là các bài tập trong mục 1 trang 73, 74, 75, 76.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Hình 1a là hình ảnh của một thước vẽ truyền
Video hướng dẫn giải
Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4cm và 5cm. Tìm độ dài hai cạnh còn lại.
Phương pháp giải:
Áp dụng tính chất của hình bình hành
Lời giải chi tiết:
Mắt lướt bóng chuyền có các cạnh đối song song nên mắt lưới có dạng hình bình hành
Vậy độ dài hai cạnh còn lại lần lượt bằng 4cm và 5cm
Video hướng dẫn giải
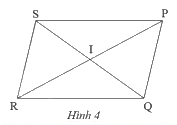
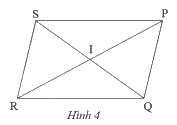
Cho hình bình hành \(PQRS\) với \(I\) là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.
Phương pháp giải:
Áp dụng tính chất của hình bình hành
Lời giải chi tiết:
Trong hình bình hành \(PQRS\) với \(I\) là giao điểm của hai đường chéo, ta có:
\(IS = IQ\); \(IP = IR\); \(PS = QR\); \(SR = PQ\)
\(\widehat {{\rm{RSP}}} = \widehat {{\rm{RQP}}}\); \(\widehat {{\rm{SRQ}}} = \widehat {{\rm{SPQ}}}\)
Video hướng dẫn giải
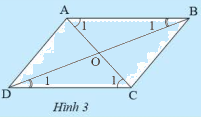
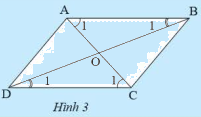
Cho tứ giác \(ABCD\) có các cạnh đối song song. Gọi \(O\) là giao điểm của hai đường chéo. Hãy chứng tỏ:
- Tam giác \(ABC\) bằng tam giác \(CDA\)
- Tam giác \(OAB\) bằng tam giác \(OCD\)
Phương pháp giải:
Áp dụng tính chất của hai đường thẳng song song
Áp dụng trường hợp bằng nhau thứ 2 của tam giác
Lời giải chi tiết:
Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))
\(AC\) chung
\(\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}\) (do \(AD\) // \(BC\))
Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c)
Xét \(\Delta OAB\) và \(\Delta OCD\) ta có:
\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))
AB = CD (do \(\Delta ABC = \Delta CDA\))
\(\widehat {{{\rm{B}}_{\rm{1}}}} = \widehat {{{\rm{D}}_{\rm{1}}}}\) (do \(\Delta ABC = \Delta CDA\))
Suy ra: \(\Delta OAB = \Delta OCD\) (g-c-g)
Video hướng dẫn giải
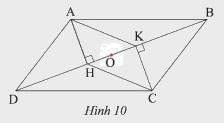
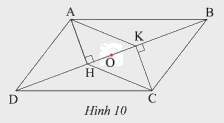
Quan sát Hình 10, cho biết \(ABCD\) và \(AKCD\) đều là hình bình hành. Chứng minh ba đoạn thẳng \(AC\), \(BD\) và \(HK\) có cùng trung điểm \(O\).
Phương pháp giải:
Sử dụng tính chất của hình bình hành
Lời giải chi tiết:
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\) (1)
Vì \(AKCH\) là hình bình hành (gt)
Mà \(O\) là trung điểm của \(AC\)
Suy ra \(O\) là trung điểm của \(HK\)
Video hướng dẫn giải
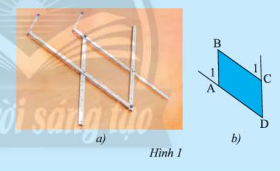
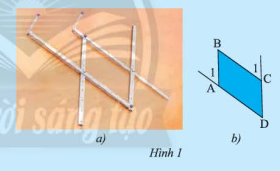
Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) của tứ giác \(ABCD\) (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh \(AB\) và \(CD\); \(AD\) và \(BC\).
Phương pháp giải:
Sử dụng thước đo góc đo số đo các góc theo yêu cầu
Sử dụng kiến thức chỉ ra các cặp đường thẳng song song
Lời giải chi tiết:
Sau khi đo góc ta thấy cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) bằng nhau
Mà các góc ở vị trí đồng vị
Suy ra: \(AB\) // \(CD\); \(AD\) // \(BC\)
Video hướng dẫn giải
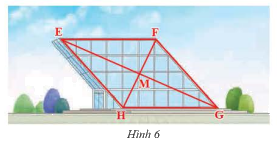
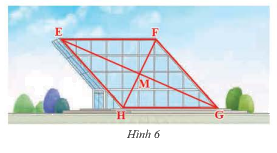
Mặt trước của một công trình xây dựng được làm bằng kính có dạng hình bình hành \(EFGH\) với \(M\) là giao điểm của hai đường chéo (Hình 6). Cho biết \(EF = 40\)m, \(EM = 36\)m, \(HM = 16\)m. Tính độ dài cạnh \(HG\) và độ dài hai đường chéo.
Phương pháp giải:
Sử dụng tính chất hình hình hành để tính các cạnh theo yêu cầu
Lời giải chi tiết:
Vì \(EFGH\) là hình bình hành
Suy ra: \(EF = HG = 40\)m; \(EM = MG = 36\)m; \(HM = MF = 16\)m
Suy ra: \(EG = 72\)m; \(HF = 32\)m
Video hướng dẫn giải
Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) của tứ giác \(ABCD\) (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh \(AB\) và \(CD\); \(AD\) và \(BC\).
Phương pháp giải:
Sử dụng thước đo góc đo số đo các góc theo yêu cầu
Sử dụng kiến thức chỉ ra các cặp đường thẳng song song
Lời giải chi tiết:
Sau khi đo góc ta thấy cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) bằng nhau
Mà các góc ở vị trí đồng vị
Suy ra: \(AB\) // \(CD\); \(AD\) // \(BC\)
Video hướng dẫn giải
Cho tứ giác \(ABCD\) có các cạnh đối song song. Gọi \(O\) là giao điểm của hai đường chéo. Hãy chứng tỏ:
- Tam giác \(ABC\) bằng tam giác \(CDA\)
- Tam giác \(OAB\) bằng tam giác \(OCD\)
Phương pháp giải:
Áp dụng tính chất của hai đường thẳng song song
Áp dụng trường hợp bằng nhau thứ 2 của tam giác
Lời giải chi tiết:
Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))
\(AC\) chung
\(\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}\) (do \(AD\) // \(BC\))
Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c)
Xét \(\Delta OAB\) và \(\Delta OCD\) ta có:
\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))
AB = CD (do \(\Delta ABC = \Delta CDA\))
\(\widehat {{{\rm{B}}_{\rm{1}}}} = \widehat {{{\rm{D}}_{\rm{1}}}}\) (do \(\Delta ABC = \Delta CDA\))
Suy ra: \(\Delta OAB = \Delta OCD\) (g-c-g)
Video hướng dẫn giải
Cho hình bình hành \(PQRS\) với \(I\) là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.
Phương pháp giải:
Áp dụng tính chất của hình bình hành
Lời giải chi tiết:
Trong hình bình hành \(PQRS\) với \(I\) là giao điểm của hai đường chéo, ta có:
\(IS = IQ\); \(IP = IR\); \(PS = QR\); \(SR = PQ\)
\(\widehat {{\rm{RSP}}} = \widehat {{\rm{RQP}}}\); \(\widehat {{\rm{SRQ}}} = \widehat {{\rm{SPQ}}}\)
Video hướng dẫn giải
Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4cm và 5cm. Tìm độ dài hai cạnh còn lại.
Phương pháp giải:
Áp dụng tính chất của hình bình hành
Lời giải chi tiết:
Mắt lướt bóng chuyền có các cạnh đối song song nên mắt lưới có dạng hình bình hành
Vậy độ dài hai cạnh còn lại lần lượt bằng 4cm và 5cm
Video hướng dẫn giải
Mặt trước của một công trình xây dựng được làm bằng kính có dạng hình bình hành \(EFGH\) với \(M\) là giao điểm của hai đường chéo (Hình 6). Cho biết \(EF = 40\)m, \(EM = 36\)m, \(HM = 16\)m. Tính độ dài cạnh \(HG\) và độ dài hai đường chéo.
Phương pháp giải:
Sử dụng tính chất hình hình hành để tính các cạnh theo yêu cầu
Lời giải chi tiết:
Vì \(EFGH\) là hình bình hành
Suy ra: \(EF = HG = 40\)m; \(EM = MG = 36\)m; \(HM = MF = 16\)m
Suy ra: \(EG = 72\)m; \(HF = 32\)m
Video hướng dẫn giải
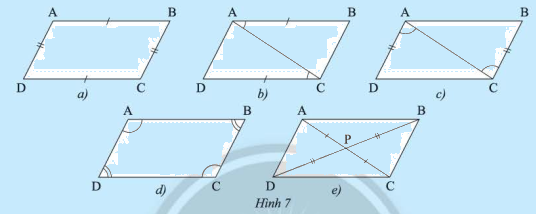
Cho tứ giác \(ABCD\) có \(P\) là giao điểm của hai đường chéo. Giải thích tại sao \(AB\) // \(CD\) và \(AD\) // \(BC\) trong mỗi trường hợp sau:
Trường hợp 1: \(AB = CD\) và \(AD = BC\) (Hình 7a)
Trường hợp 2: \(AB\) // \(CD\) và \(AB = CD\) (Hình 7b)
Trường hợp 3: \(AD\) // \(BC\) và \(AD = BC\) (Hình 7c)
Trường hợp 4: \(\widehat {\rm{A}} = \widehat {\rm{C}}\), \(\widehat {\rm{B}} = \widehat {\rm{D}}\) (Hình 7d)
Trường hợp 5: \(PA = PC\), \(PB = PD\) (Hình 7e)
Phương pháp giải:
Chứng minh các góc ở vị trí trong cùng phía bù nhau, so le trong bằng nhau
Lời giải chi tiết:
a) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(AB = CD\) (gt)
\(AD = BC\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta CDA\) (c-c-c)
\( \Rightarrow \widehat {BAC} = \widehat {ACD}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\) // \(CD\)
Chứng minh tương tự \(\Delta ADB = \Delta CBD\) (c-c-c)
\( \Rightarrow \widehat {ABD} = \widehat {CDB}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong \( \Rightarrow AD\;{\rm{//}}\;BC\)
b) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(AB = CD\) (gt)
\(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) (do \(AB\) // \(CD\))
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c)
\( \Rightarrow \widehat {BCA} = \widehat {CAD}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AD\;{\rm{//}}\;BC\)
c) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(BC = AD\) (gt)
\(\widehat {{\rm{BCA}}} = \widehat {{\rm{CDA}}}\) (do \(AD\) // \(BC\))
\(AC\) chung
Suy ra \(\Delta ABC = \Delta CDA\) (c-g-c)
Suy ra \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra: \(AB\) // \(CD\)
d) Xét tứ giác \(ABCD\) ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Mà \(\widehat A = \widehat C\); \(\widehat B = \widehat D\) (gt)
Suy ra \(\widehat A + \widehat D = 180^\circ ;\;\widehat A + \widehat B = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(AB\;{\rm{//}}\;CD;\;AD\;{\rm{//}}\;BC\)
e) Xét \(\Delta APB\) và \(\Delta CPD\) ta có:
\(PA = PC\) (gt)
\(\widehat {{\rm{APB}}} = \widehat {{\rm{CPD}}}\) (đối đỉnh)
\(PB = PD\) (gt)
Suy ra: \(\Delta APB = \Delta CPD\) (c-g-c)
Suy ra: \(\widehat {BAP} = \widehat {PCD}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\;{\rm{//}}\;CD\)
Chứng minh tương tự: \(\Delta APD = \Delta CPB\) (c-g-c)
Suy ra \(\widehat {{\rm{DAP}}} = \widehat {{\rm{BCP}}}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AD\) // \(BC\)
Video hướng dẫn giải
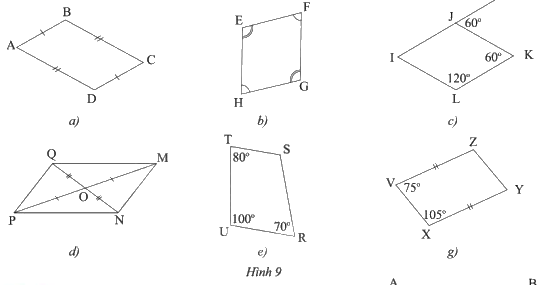
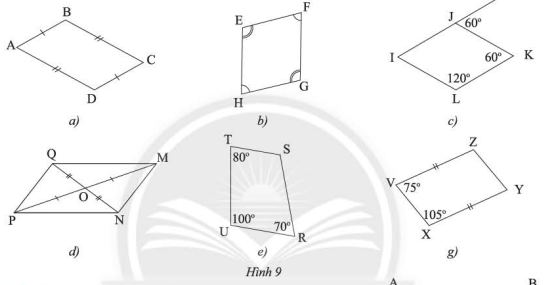
Trong các tứ giác ở Hình 9, tứ giác nào không là hình bình hành?
Phương pháp giải:
Sử dụng dấu hiệu nhận biết hình bình hành
Lời giải chi tiết:
a) Xét tứ giác \(ABCD\) ta có:
\(AB = CD\) (gt)
\(AD = BC\) (gt)
Suy ra: \(ABCD\) là hình bình hành
b) Xét tứ giác \(EFGH\) ta có:
\(\widehat {\rm{E}} = \widehat G\) (gt)
\(\widehat F = \widehat H\) (gt)
Suy ra \(EFGH\) là hình bình hành
c) Ta có: \(\widehat J = \widehat {\rm{K}} = 60^\circ \) (gt)
Mà hai góc ở vị trí so le trong
Suy ra \(IJ\) // \(KL\) (1)
Ta có: \(\widehat K + \widehat L = 60^\circ + 120^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(JK\;{\rm{//}}\;IL\) (2)
Từ (1), (2) suy ra \(IJKL\) là hình bình hành
d) Xét tứ giác \(MNPQ\) ta có:
\(O\) là trung điểm của \(NQ\) (do \(OQ = ON\))
\(O\) là trung điểm của \(MP\) (do \(OP = OM\))
Suy ra \(MNPQ\) là hình bình hành
e) Tứ giác \(TSRU\) không là hình bình hành
g) Ta có: \(\widehat {\rm{V}} + \widehat {\rm{X}} = 75^\circ + 105^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra: \(VZ\) // \(XY\)
Xét tứ giác \(VZYX\) ta có:
\(VZ\) // \(XY\) (cmt)
\(VZ = XY\) (gt)
Suy ra \(VZYX\) là hình bình hành
Video hướng dẫn giải
Quan sát Hình 10, cho biết \(ABCD\) và \(AKCD\) đều là hình bình hành. Chứng minh ba đoạn thẳng \(AC\), \(BD\) và \(HK\) có cùng trung điểm \(O\).
Phương pháp giải:
Sử dụng tính chất của hình bình hành
Lời giải chi tiết:
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\) (1)
Vì \(AKCH\) là hình bình hành (gt)
Mà \(O\) là trung điểm của \(AC\)
Suy ra \(O\) là trung điểm của \(HK\)
Video hướng dẫn giải
Trong các tứ giác ở Hình 9, tứ giác nào không là hình bình hành?
Phương pháp giải:
Sử dụng dấu hiệu nhận biết hình bình hành
Lời giải chi tiết:
a) Xét tứ giác \(ABCD\) ta có:
\(AB = CD\) (gt)
\(AD = BC\) (gt)
Suy ra: \(ABCD\) là hình bình hành
b) Xét tứ giác \(EFGH\) ta có:
\(\widehat {\rm{E}} = \widehat G\) (gt)
\(\widehat F = \widehat H\) (gt)
Suy ra \(EFGH\) là hình bình hành
c) Ta có: \(\widehat J = \widehat {\rm{K}} = 60^\circ \) (gt)
Mà hai góc ở vị trí so le trong
Suy ra \(IJ\) // \(KL\) (1)
Ta có: \(\widehat K + \widehat L = 60^\circ + 120^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(JK\;{\rm{//}}\;IL\) (2)
Từ (1), (2) suy ra \(IJKL\) là hình bình hành
d) Xét tứ giác \(MNPQ\) ta có:
\(O\) là trung điểm của \(NQ\) (do \(OQ = ON\))
\(O\) là trung điểm của \(MP\) (do \(OP = OM\))
Suy ra \(MNPQ\) là hình bình hành
e) Tứ giác \(TSRU\) không là hình bình hành
g) Ta có: \(\widehat {\rm{V}} + \widehat {\rm{X}} = 75^\circ + 105^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra: \(VZ\) // \(XY\)
Xét tứ giác \(VZYX\) ta có:
\(VZ\) // \(XY\) (cmt)
\(VZ = XY\) (gt)
Suy ra \(VZYX\) là hình bình hành
Video hướng dẫn giải
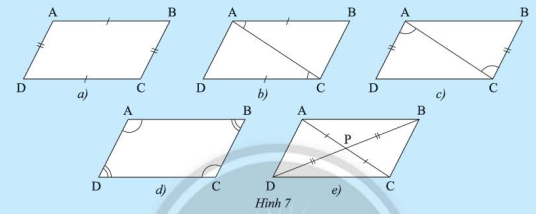
Cho tứ giác \(ABCD\) có \(P\) là giao điểm của hai đường chéo. Giải thích tại sao \(AB\) // \(CD\) và \(AD\) // \(BC\) trong mỗi trường hợp sau:
Trường hợp 1: \(AB = CD\) và \(AD = BC\) (Hình 7a)
Trường hợp 2: \(AB\) // \(CD\) và \(AB = CD\) (Hình 7b)
Trường hợp 3: \(AD\) // \(BC\) và \(AD = BC\) (Hình 7c)
Trường hợp 4: \(\widehat {\rm{A}} = \widehat {\rm{C}}\), \(\widehat {\rm{B}} = \widehat {\rm{D}}\) (Hình 7d)
Trường hợp 5: \(PA = PC\), \(PB = PD\) (Hình 7e)
Phương pháp giải:
Chứng minh các góc ở vị trí trong cùng phía bù nhau, so le trong bằng nhau
Lời giải chi tiết:
a) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(AB = CD\) (gt)
\(AD = BC\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta CDA\) (c-c-c)
\( \Rightarrow \widehat {BAC} = \widehat {ACD}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\) // \(CD\)
Chứng minh tương tự \(\Delta ADB = \Delta CBD\) (c-c-c)
\( \Rightarrow \widehat {ABD} = \widehat {CDB}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong \( \Rightarrow AD\;{\rm{//}}\;BC\)
b) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(AB = CD\) (gt)
\(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) (do \(AB\) // \(CD\))
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c)
\( \Rightarrow \widehat {BCA} = \widehat {CAD}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AD\;{\rm{//}}\;BC\)
c) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(BC = AD\) (gt)
\(\widehat {{\rm{BCA}}} = \widehat {{\rm{CDA}}}\) (do \(AD\) // \(BC\))
\(AC\) chung
Suy ra \(\Delta ABC = \Delta CDA\) (c-g-c)
Suy ra \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra: \(AB\) // \(CD\)
d) Xét tứ giác \(ABCD\) ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Mà \(\widehat A = \widehat C\); \(\widehat B = \widehat D\) (gt)
Suy ra \(\widehat A + \widehat D = 180^\circ ;\;\widehat A + \widehat B = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(AB\;{\rm{//}}\;CD;\;AD\;{\rm{//}}\;BC\)
e) Xét \(\Delta APB\) và \(\Delta CPD\) ta có:
\(PA = PC\) (gt)
\(\widehat {{\rm{APB}}} = \widehat {{\rm{CPD}}}\) (đối đỉnh)
\(PB = PD\) (gt)
Suy ra: \(\Delta APB = \Delta CPD\) (c-g-c)
Suy ra: \(\widehat {BAP} = \widehat {PCD}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\;{\rm{//}}\;CD\)
Chứng minh tương tự: \(\Delta APD = \Delta CPB\) (c-g-c)
Suy ra \(\widehat {{\rm{DAP}}} = \widehat {{\rm{BCP}}}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AD\) // \(BC\)
Mục 1 của chương trình Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán cơ bản, các biểu thức đại số và các bài toán liên quan đến đa thức. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Các bài tập trên trang 73 chủ yếu tập trung vào việc thực hành các phép toán cộng, trừ, nhân, chia đa thức. Các em cần chú ý đến việc áp dụng đúng các quy tắc về dấu và thứ tự thực hiện các phép toán.
Các bài tập trên trang 74 tiếp tục củng cố kiến thức về các phép toán với đa thức, đồng thời giới thiệu thêm về các phương pháp phân tích đa thức thành nhân tử.
Trang 75 tập trung vào việc giải các phương trình bậc nhất một ẩn. Các em cần nắm vững các bước giải phương trình và kiểm tra lại nghiệm.
| Bài tập | Nội dung |
|---|---|
| Bài 7 | Giải phương trình: 2x + 5 = 11 |
| Bài 8 | Giải phương trình: 3(x - 2) = 9 |
| Bài 9 | Giải bài toán thực tế dẫn đến phương trình bậc nhất một ẩn. |
Các bài tập trên trang 76 là sự kết hợp của các kiến thức đã học, đòi hỏi các em phải vận dụng linh hoạt và sáng tạo để giải quyết.
Bài 10: Tìm x sao cho biểu thức A = (x - 1)(x + 2) đạt giá trị nhỏ nhất.
Bài 11: Giải bài toán về chuyển động với vận tốc và thời gian.
Bài 12: Giải bài toán về năng suất lao động.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 73, 74, 75, 76 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc các em học tập tốt!