Bài 11 trang 59 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 11 trang 59 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
a) Độ cao
Đề bài
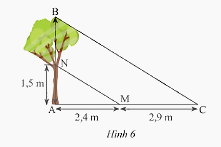
a) Độ cao \(AN\) và chiều dài bóng nắng của các đoạn thẳng \(AN,BN\) trên mặt đất được ghi lại như trong Hình 6. Tính chiều cao \(AB\) của cái cây.
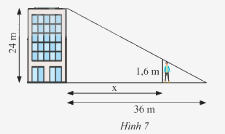
b) Một tòa nhà cao 24m, đổ bóng nắng dài 36m trên đường như Hình 7. Một người cao 1,6m muốn đứng trong bóng dâm của toàn nhà. Hỏi người đó có thể đứng cách tòa nhà xa nhất là bao nhiêu mét?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết
a) Xét tam giác \(ABC\) có \(MN//BC\) nên theo định lí Thales ta có:
\(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} \\\frac{{1,5}}{{AB}} = \frac{{2,4}}{{2,4 + 2,9}}\)
suy ra \(AB = \frac{{1,5.\left( {2,4 + 2,9} \right)}}{{2,4}} = 3,3125\)
Vậy chiều cao \(AB\) của cái cây là 3,3125m.
b) Đặt tên các điểm như hình vẽ
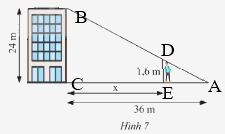
Xét tam giác \(ABC\) có \(DE//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} = \frac{{AC - CE}}{{AC}} \\ \frac{{1,6}}{{24}} = \frac{{36 - x}}{{36}}\)
suy ra \(36 - x = \frac{{1,6.36}}{{24}} \)
nên \(x = 36 - \frac{{1,6.36}}{{24}} = 33,6\)
Vậy người đó có thể đứng xa tòa nhà nhất là 33,6m.
Bài 11 trang 59 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số, đặc biệt là các quy tắc cộng, trừ, nhân, chia đa thức để giải quyết bài toán. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và phương pháp giải quyết bài toán.
Bài 11 thường xoay quanh việc thực hiện các phép toán với đa thức, ví dụ như:
Để giải bài 11 trang 59 SGK Toán 8 tập 2, học sinh có thể áp dụng các phương pháp sau:
Giả sử bài tập yêu cầu rút gọn biểu thức: (x + 2)(x - 2) + x2
Lời giải:
(x + 2)(x - 2) + x2 = x2 - 4 + x2 = 2x2 - 4
Khi giải bài tập về đại số, học sinh cần chú ý:
Để rèn luyện thêm kỹ năng giải bài tập đại số, học sinh có thể tham khảo các bài tập tương tự trong SGK Toán 8 tập 2 và các tài liệu tham khảo khác.
Bài 11 trang 59 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bằng cách nắm vững kiến thức và phương pháp giải quyết bài toán, học sinh có thể tự tin hơn trong quá trình học tập môn Toán.
| Công thức | Mô tả |
|---|---|
| (a + b)2 = a2 + 2ab + b2 | Bình phương của một tổng |
| (a - b)2 = a2 - 2ab + b2 | Bình phương của một hiệu |
| a2 - b2 = (a + b)(a - b) | Hiệu hai bình phương |