Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 70, 71 sách giáo khoa Toán 8 Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học và hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 8 và đạt kết quả tốt nhất trong học tập.
Cho hình thang
Video hướng dẫn giải
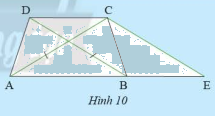
Cho hình thang \(ABCD\) có hai đáy là \(AB\), \(CD\) và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua \(C\), song song với \(BD\) và cắt \(AB\) tại \(E\).
a) Tam giác \(CAE\) là tam giác gì? Vì sao?
b) So sánh tam giác \(ABD\) và tam giác \(BAC\)
Phương pháp giải:
Sử dụng tính chất của hình thang cân chứng minh \(\Delta CAE\) cân; \(\Delta ABD = \Delta BAC\)
Lời giải chi tiết:
a) Vì \(ABCD\) là hình thang cân (gt)
\( \Rightarrow AC = BD\) và \(AB\;{\rm{//}}\;CD\)
Xét \(\Delta BCD\) và \(\Delta CBE\) ta có:
\(\widehat {DCB} = \widehat {CBE}\) (do \(AB\) // \(CD\))
\(BC\) chung
\(\widehat {CBD} = \widehat {BCE}\) (do \(CE\) // \(BD\))
Suy ra \(\Delta BCD = \Delta CBE\) (g-c-g)
Suy ra \(BD = CE\) (hai cạnh tương ứng)
Mà \(AC = BD\) (cmt)
Suy ra \(AC = EC\)
Suy ra \(\Delta CAE\) cân tại \(C\)
b) Xét \(\Delta ABD\) và \(\Delta BAC\) ta có:
\(DA = BC\) (do \(ABCD\) là hình thang cân)
\(\widehat {DAB} = \widehat {CBA}\) (Do \(ABCD\) là hình thang cân)
\(AB\) chung
Suy ra \(\Delta ABD = \Delta BAC\) (c-g-c)
Video hướng dẫn giải
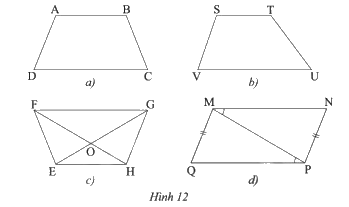
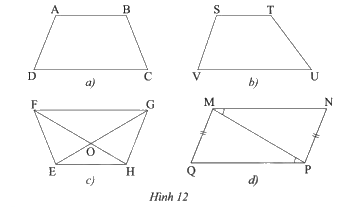
Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12.
Phương pháp giải:
Sử dụng thước đo góc và đo độ dài và dấu hiệu nhận biết để tìm hình thang cân
Lời giải chi tiết:
Sau khi đo độ dài các cạnh và các góc, ta thấy \(ABCD\), \(EFGH\) là các hình thang cân.
Video hướng dẫn giải
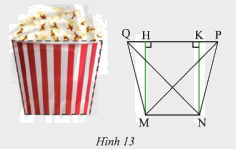
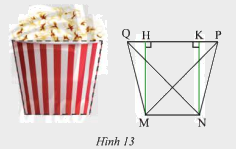
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân \(MNPQ\) (Hình 13) với hai đáy \(MN = 6cm\), \(PQ = 10\)cm và độ dài hai đường chéo \(MN = NQ = 8\sqrt 2 \) cm. Tính độ dài đường chéo và cạnh bên của hình thang
Phương pháp giải:
Chứng minh \(QH = KP\)
Tính độ dài các đoạn thẳng \(HK\), \(QH\), \(KP\)
Áp dụng định lý Pythagore tính độ dài \(MH\), \(MQ\)
Lời giải chi tiết:
a) Xét \(\Delta MHQ\) và \(\Delta NKP\) ta có:
\(\widehat {MHQ} = \widehat {NKP} = 90^\circ \)
\(MQ = NP\) (do \(MNPQ\) là hình thang cân)
\(\widehat {MQP} = \widehat {NPQ}\) (do \(MNPQ\) là hình thang cân)
Suy ra: \(\Delta MHQ = \Delta NKP\) (ch – gn)
Suy ra: \(HQ = KP\) (hai cạnh tương ứng)
Suy ra \(HQ = KP = \frac{{PQ - HK}}{2} = \frac{{10 - 6}}{2} = 2\) (cm)
\(HP = 8\)cm
Áp dụng định lý Pythagore vào tam giác vuông \(MHP\) ta có:
\(M{H^2} = M{P^2} - H{P^2} = {\left( {8\sqrt 2 } \right)^2} - {8^2} = 128 - 64 = 64\)
\(MH = 8\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(MHQ\) ta có:
\(M{Q^2} = M{H^2} + Q{H^2} = {8^2} + {2^2} = 68\)
\(MQ = \sqrt {68} \) (cm)
Video hướng dẫn giải
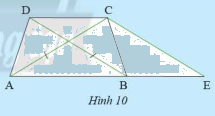
Cho hình thang \(ABCD\) có hai đáy là \(AB\), \(CD\) và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua \(C\), song song với \(BD\) và cắt \(AB\) tại \(E\).
a) Tam giác \(CAE\) là tam giác gì? Vì sao?
b) So sánh tam giác \(ABD\) và tam giác \(BAC\)
Phương pháp giải:
Sử dụng tính chất của hình thang cân chứng minh \(\Delta CAE\) cân; \(\Delta ABD = \Delta BAC\)
Lời giải chi tiết:
a) Vì \(ABCD\) là hình thang cân (gt)
\( \Rightarrow AC = BD\) và \(AB\;{\rm{//}}\;CD\)
Xét \(\Delta BCD\) và \(\Delta CBE\) ta có:
\(\widehat {DCB} = \widehat {CBE}\) (do \(AB\) // \(CD\))
\(BC\) chung
\(\widehat {CBD} = \widehat {BCE}\) (do \(CE\) // \(BD\))
Suy ra \(\Delta BCD = \Delta CBE\) (g-c-g)
Suy ra \(BD = CE\) (hai cạnh tương ứng)
Mà \(AC = BD\) (cmt)
Suy ra \(AC = EC\)
Suy ra \(\Delta CAE\) cân tại \(C\)
b) Xét \(\Delta ABD\) và \(\Delta BAC\) ta có:
\(DA = BC\) (do \(ABCD\) là hình thang cân)
\(\widehat {DAB} = \widehat {CBA}\) (Do \(ABCD\) là hình thang cân)
\(AB\) chung
Suy ra \(\Delta ABD = \Delta BAC\) (c-g-c)
Video hướng dẫn giải
Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12.
Phương pháp giải:
Sử dụng thước đo góc và đo độ dài và dấu hiệu nhận biết để tìm hình thang cân
Lời giải chi tiết:
Sau khi đo độ dài các cạnh và các góc, ta thấy \(ABCD\), \(EFGH\) là các hình thang cân.
Video hướng dẫn giải
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân \(MNPQ\) (Hình 13) với hai đáy \(MN = 6cm\), \(PQ = 10\)cm và độ dài hai đường chéo \(MN = NQ = 8\sqrt 2 \) cm. Tính độ dài đường chéo và cạnh bên của hình thang
Phương pháp giải:
Chứng minh \(QH = KP\)
Tính độ dài các đoạn thẳng \(HK\), \(QH\), \(KP\)
Áp dụng định lý Pythagore tính độ dài \(MH\), \(MQ\)
Lời giải chi tiết:
a) Xét \(\Delta MHQ\) và \(\Delta NKP\) ta có:
\(\widehat {MHQ} = \widehat {NKP} = 90^\circ \)
\(MQ = NP\) (do \(MNPQ\) là hình thang cân)
\(\widehat {MQP} = \widehat {NPQ}\) (do \(MNPQ\) là hình thang cân)
Suy ra: \(\Delta MHQ = \Delta NKP\) (ch – gn)
Suy ra: \(HQ = KP\) (hai cạnh tương ứng)
Suy ra \(HQ = KP = \frac{{PQ - HK}}{2} = \frac{{10 - 6}}{2} = 2\) (cm)
\(HP = 8\)cm
Áp dụng định lý Pythagore vào tam giác vuông \(MHP\) ta có:
\(M{H^2} = M{P^2} - H{P^2} = {\left( {8\sqrt 2 } \right)^2} - {8^2} = 128 - 64 = 64\)
\(MH = 8\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(MHQ\) ta có:
\(M{Q^2} = M{H^2} + Q{H^2} = {8^2} + {2^2} = 68\)
\(MQ = \sqrt {68} \) (cm)
Mục 3 trong chương trình Toán 8 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để hoàn thành tốt các bài tập này.
Để giúp các em hiểu rõ hơn về nội dung bài tập, chúng ta sẽ đi vào phân tích từng bài tập cụ thể:
Bài tập này yêu cầu học sinh… (Giải thích chi tiết yêu cầu bài tập và cách giải). Ví dụ, bài tập có thể yêu cầu chứng minh một đẳng thức hình học, giải một phương trình bậc nhất, hoặc tính diện tích một hình. Chúng ta sẽ sử dụng các công thức và định lý đã học để giải quyết bài toán này.
Bài tập này tập trung vào… (Giải thích chi tiết yêu cầu bài tập và cách giải). Ví dụ, bài tập có thể yêu cầu tìm giá trị của một biểu thức, giải một bài toán ứng dụng, hoặc vẽ một hình theo yêu cầu. Chúng ta cần phân tích kỹ đề bài để xác định đúng phương pháp giải.
Bài tập này đòi hỏi học sinh… (Giải thích chi tiết yêu cầu bài tập và cách giải). Ví dụ, bài tập có thể yêu cầu giải một hệ phương trình, chứng minh một bất đẳng thức, hoặc tìm điều kiện để một phương trình có nghiệm. Chúng ta cần kết hợp các kiến thức đã học để giải quyết bài toán này.
Bài toán: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Giải:
Áp dụng định lý Pitago vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42 = 9 + 16 = 25
BC = √25 = 5cm
Vậy, độ dài cạnh BC là 5cm.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn khi giải bài tập mục 3 trang 70, 71 SGK Toán 8 Chân trời sáng tạo. Chúc các em học tập tốt!