Chào mừng các em học sinh đến với lời giải chi tiết bài 11 trang 96 SGK Toán 8 tập 2 – Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài 11 trang 96 thuộc chương trình Toán 8 tập 2, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
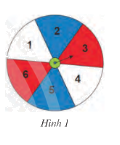
Một tấm bìa hình tròn được chia thành 6 phần bằng nhau như Hình 1
Đề bài
Một tấm bìa hình tròn được chia thành 6 phần bằng nhau như Hình 1. Bạn Thủy quay mũi tên và quan sát xem khi dừng lại mũi tên chỉ vào ô số mấy. Thủy ghi lại kết quả sau 120 lần thí nghiệm ở bảng sau:
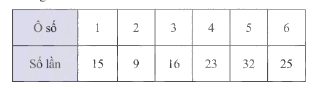
a) Tính xác suất thực nghiệm của biến cố “Mũi tên chỉ vào ô có màu trắng”.
b) Theo dự đoán, xác suất mũi tên chỉ vào mỗi ô có bằng nhau không?
c) Một người nhận định rằng xác suất mũi tên chỉ vào các ô màu xanh bằng xác suất mũi tên chỉ vào các ô màu trằng và bằng xác suất chỉ vào các ô màu đỏ. Theo em, kết quả thực nghiệm của bạn Thủy có phù hợp với nhận định đó không?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi \(P\left( A \right)\) là xác suất xuất hiện biến cố \(A\) khi thực hiện một phép thử.
Gọi \(n\left( A \right)\) là số lần xuất hiện biến cố \(A\) khi thực hiện phép thử đó \(n\) lần.
Xác suất thực nghiệm của biến cố \(A\) là tỉ số \(\frac{{n\left( A \right)}}{n}\)
Khi \(n\) càng lớn, xác suất thực nghiệm của biến cố \(A\) càng gần \(P\left( A \right)\).
Lời giải chi tiết
a) Ô màu trắng được đánh số 1 và số 4 nên số lần mũi tên chỉ vào ô màu trắng là:
\(15 + 23 = 38\) (lần)
Xác suất thực nghiệm của biến cố mũi tên chỉ vào ô có màu trắng là \(\frac{{38}}{{120}} = \frac{{19}}{{60}}\).
b) Dự đoán xác suất thực nghiệm mũi tên chỉ vào mỗi ô là không như nhau.
c) Ô màu đỏ được đánh số 3 và số 6 nên số lần mũi tên chỉ vào ô màu đỏ là:
\(16 + 25 = 41\) (lần)
Xác suất thực nghiệm của biến cố mũi tên chỉ vào ô có màu đỏ là \(\frac{{41}}{{120}}\).
Ô màu xanh được đánh số 2 và số 5 nên số lần mũi tên chỉ vào ô màu xanh là:
\(9 + 32 = 41\) (lần)
Xác suất thực nghiệm của biến cố mũi tên chỉ vào ô có màu xanh là \(\frac{{41}}{{120}}\).
Vì thực nghiệm của biến cố mũi tên chỉ vào ô màu trắng khác xác suất thực nghiệm mũi tên chỉ vào ô màu đỏ và xác suất thực nghiệm mũi tên chỉ vào ô màu xanh \(\left( {\frac{{41}}{{120}} \ne \frac{{19}}{{60}}} \right)\).
Do đó, kết quả thực nghiệm của bạn Thủy là chưa phù hợp với nhận định.
Bài 11 trang 96 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về các tứ giác đặc biệt (hình bình hành, hình chữ nhật, hình thoi, hình vuông) để giải quyết các vấn đề liên quan đến tính chất và dấu hiệu nhận biết chúng. Bài tập này không chỉ giúp học sinh củng cố lý thuyết mà còn rèn luyện kỹ năng tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Bài 11 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 11 trang 96 SGK Toán 8 tập 2 – Chân trời sáng tạo, chúng tôi xin trình bày lời giải chi tiết cho từng phần của bài tập:
Để chứng minh một tứ giác là hình bình hành, ta có thể sử dụng một trong các cách sau:
Ví dụ: Cho tứ giác ABCD có AB song song CD và AD song song BC. Chứng minh ABCD là hình bình hành.
Lời giải:
Vì AB song song CD và AD song song BC nên tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Khi đã xác định được một tứ giác là hình bình hành, hình chữ nhật, hình thoi hoặc hình vuông, ta có thể sử dụng các tính chất của chúng để tính độ dài các cạnh và số đo các góc.
Ví dụ: Cho hình chữ nhật ABCD có AB = 5cm và BC = 3cm. Tính độ dài đường chéo AC.
Lời giải:
Vì ABCD là hình chữ nhật nên góc ABC vuông. Áp dụng định lý Pitago vào tam giác ABC, ta có:
AC2 = AB2 + BC2 = 52 + 32 = 25 + 9 = 34
Suy ra AC = √34 cm.
Các bài toán thực tế thường yêu cầu học sinh vận dụng kiến thức về tứ giác đặc biệt để giải quyết các vấn đề liên quan đến hình học trong đời sống.
Ví dụ: Một mảnh đất hình chữ nhật có chiều dài 12m và chiều rộng 8m. Người ta muốn xây một con đường đi chéo qua mảnh đất đó. Hỏi con đường đó dài bao nhiêu mét?
Lời giải:
Con đường đi chéo qua mảnh đất hình chữ nhật chính là đường chéo của hình chữ nhật đó. Áp dụng định lý Pitago vào tam giác tạo bởi chiều dài, chiều rộng và đường chéo, ta có:
Đường chéo2 = Chiều dài2 + Chiều rộng2 = 122 + 82 = 144 + 64 = 208
Suy ra đường chéo = √208 ≈ 14.42m.
Bài 11 trang 96 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về các tứ giác đặc biệt. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin giải quyết bài tập này một cách hiệu quả. Chúc các em học tốt!