Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 69, 70 sách giáo khoa Toán 8 Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
a) Cho hình thang cân
Video hướng dẫn giải
Tìm các đoạn thẳng bằng nhau trong hình thang cân \(MNPQ\) có hai đáy \(MN\) và \(PQ\)
Phương pháp giải:
Sử dụng tính chất của hình thang cân.
Lời giải chi tiết:
Vì \(MNPQ\) là hình thang cân (gt)
Suy ra: \(MP = NQ\) và \(MQ = NP\)
Video hướng dẫn giải
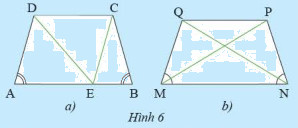
a) Cho hình thang cân \(ABCD\) có hai đáy là \(AB\) và \(CD\) (\(AB > CD\). Qua \(C\) vẽ đường thẳng song song với \(AD\) và cắt \(AB\) tại \(E\) (Hình 6a)
i) Tam giác \(CEB\) là tam giác gì? Vì sao?
ii) So sánh \(AD\) và \(BC\)
b) Cho hình thang cân \(MNPQ\) có hai đáy là \(MN\) và \(PQ\) (Hình 6). So sánh \(MP\) và \(NQ\)
Phương pháp giải:
Sử dụng kiến thức về góc tạo bởi hai đường thẳng song song (góc đồng vị) và định nghĩa hình thang cân để chỉ ra \(\widehat {CEB} = \widehat {CBE}\) (do cùng bằng \(\widehat {{\rm{DAE}}}\))
Lời giải chi tiết:
a) i) \(ABCD\) là hình thang cân (gt)
\( \Rightarrow \widehat A = \widehat B\) (1) và \(DC\) // \(AE\)
Vì \(AD\;{\rm{//}}\;CE\) (gt)
\(\widehat A = \widehat {CEB}\) (cặp góc đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {CEB} = \widehat B\)
Suy ra \(\Delta CEB\) là tam giác cân.
ii) \(\Delta CEB\) cân tại \(C\) (cmt)
Suy ra: \(CE = BC\) (3)
Xét \(\Delta ADE\) và \(\Delta CED\) ta có:
\(\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}\) (\(AD\)// \(CE\), cặp góc so le trong)
\(DE\) chung
\(\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}\) (\(CD\) // \(AB\), cặp góc so le trong)
Suy ra: \(\Delta ADE = \Delta CED\) (g-c-g)
Suy ra: \(AD = CE\) (4)
Từ (3) và (4) suy ra: \(AD = BC\)
b) Chứng minh tương tự như ý a) ta có: Hình thang cân \(MNPQ\) có hai cạnh bên \(MQ = NP\)
Xét tam giác \(\Delta MQP\) và \(\Delta NPQ\) ta có:
\(MQ = NP\) (cmt)
\(\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}\) (do \(MNPQ\) là hình thang cân)
\(PQ\) chung
Suy ra: \(\Delta MQP = \Delta NPQ\) (c-g-c)
\( \Rightarrow MP = NQ\) (hai cạnh tương ứng)
Video hướng dẫn giải
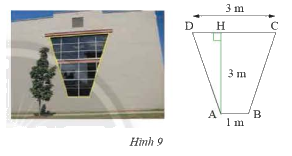
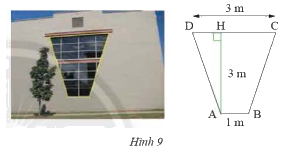
Một khung cửa sổ hình thang cân có chiều cao 3m, hai đáy là 3m và 1m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.
Phương pháp giải:
Kẻ đường cao \(BK\)
Sử dụng tính chất của hình thang cân
Lời giải chi tiết:
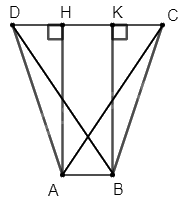
Kẻ đường cao \(BK\)
Suy ra \(AH = BK\) và \(AHKB\) là hình chữ nhật
Suy ra \(HK = AB = 1\)cm
Vì \(ABCD\) là hình thang cân (gt)
\( \Rightarrow AC = BD\) và \(AD = BC\)(tc)
Xét \(\Delta AHD\) và \(\Delta BKC\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{BKC}}} = 90^\circ \) (gt)
\(\widehat D = \widehat C\) (định nghĩa hình thang cân)
\(AD = BC\) (tính chất hình thang cân)
Suy ra: \(\Delta AHD = \Delta BKC\) (ch – gn)
Suy ra \(DH = KC\) (hai cạnh tương ứng)
Suy ra \(DH = KC = \frac{{CD - HK}}{2} = \frac{{3 - 1}}{2} = 1\) (cm)
Suy ra \(HC = 2\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(AHD\) ta có:
\(A{D^2} = D{H^2} + A{H^2} = {1^2} + {3^2} = 10\)
Suy ra \(AD = \sqrt {10} \) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(ACH\) ta có:
\(A{C^2} = A{H^2} + H{C^2} = {3^2} + {2^2} = 9 + 4 = 13\)
\(AC = \sqrt {13} \) (cm)
Vậy \(AC = BD = \sqrt {13} \)cm; \(AD = BC = \sqrt {10} \) cm
Video hướng dẫn giải
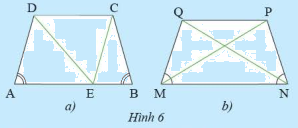
a) Cho hình thang cân \(ABCD\) có hai đáy là \(AB\) và \(CD\) (\(AB > CD\). Qua \(C\) vẽ đường thẳng song song với \(AD\) và cắt \(AB\) tại \(E\) (Hình 6a)
i) Tam giác \(CEB\) là tam giác gì? Vì sao?
ii) So sánh \(AD\) và \(BC\)
b) Cho hình thang cân \(MNPQ\) có hai đáy là \(MN\) và \(PQ\) (Hình 6). So sánh \(MP\) và \(NQ\)
Phương pháp giải:
Sử dụng kiến thức về góc tạo bởi hai đường thẳng song song (góc đồng vị) và định nghĩa hình thang cân để chỉ ra \(\widehat {CEB} = \widehat {CBE}\) (do cùng bằng \(\widehat {{\rm{DAE}}}\))
Lời giải chi tiết:
a) i) \(ABCD\) là hình thang cân (gt)
\( \Rightarrow \widehat A = \widehat B\) (1) và \(DC\) // \(AE\)
Vì \(AD\;{\rm{//}}\;CE\) (gt)
\(\widehat A = \widehat {CEB}\) (cặp góc đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {CEB} = \widehat B\)
Suy ra \(\Delta CEB\) là tam giác cân.
ii) \(\Delta CEB\) cân tại \(C\) (cmt)
Suy ra: \(CE = BC\) (3)
Xét \(\Delta ADE\) và \(\Delta CED\) ta có:
\(\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}\) (\(AD\)// \(CE\), cặp góc so le trong)
\(DE\) chung
\(\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}\) (\(CD\) // \(AB\), cặp góc so le trong)
Suy ra: \(\Delta ADE = \Delta CED\) (g-c-g)
Suy ra: \(AD = CE\) (4)
Từ (3) và (4) suy ra: \(AD = BC\)
b) Chứng minh tương tự như ý a) ta có: Hình thang cân \(MNPQ\) có hai cạnh bên \(MQ = NP\)
Xét tam giác \(\Delta MQP\) và \(\Delta NPQ\) ta có:
\(MQ = NP\) (cmt)
\(\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}\) (do \(MNPQ\) là hình thang cân)
\(PQ\) chung
Suy ra: \(\Delta MQP = \Delta NPQ\) (c-g-c)
\( \Rightarrow MP = NQ\) (hai cạnh tương ứng)
Video hướng dẫn giải
Tìm các đoạn thẳng bằng nhau trong hình thang cân \(MNPQ\) có hai đáy \(MN\) và \(PQ\)
Phương pháp giải:
Sử dụng tính chất của hình thang cân.
Lời giải chi tiết:
Vì \(MNPQ\) là hình thang cân (gt)
Suy ra: \(MP = NQ\) và \(MQ = NP\)
Video hướng dẫn giải
Một khung cửa sổ hình thang cân có chiều cao 3m, hai đáy là 3m và 1m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.
Phương pháp giải:
Kẻ đường cao \(BK\)
Sử dụng tính chất của hình thang cân
Lời giải chi tiết:
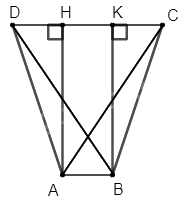
Kẻ đường cao \(BK\)
Suy ra \(AH = BK\) và \(AHKB\) là hình chữ nhật
Suy ra \(HK = AB = 1\)cm
Vì \(ABCD\) là hình thang cân (gt)
\( \Rightarrow AC = BD\) và \(AD = BC\)(tc)
Xét \(\Delta AHD\) và \(\Delta BKC\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{BKC}}} = 90^\circ \) (gt)
\(\widehat D = \widehat C\) (định nghĩa hình thang cân)
\(AD = BC\) (tính chất hình thang cân)
Suy ra: \(\Delta AHD = \Delta BKC\) (ch – gn)
Suy ra \(DH = KC\) (hai cạnh tương ứng)
Suy ra \(DH = KC = \frac{{CD - HK}}{2} = \frac{{3 - 1}}{2} = 1\) (cm)
Suy ra \(HC = 2\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(AHD\) ta có:
\(A{D^2} = D{H^2} + A{H^2} = {1^2} + {3^2} = 10\)
Suy ra \(AD = \sqrt {10} \) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(ACH\) ta có:
\(A{C^2} = A{H^2} + H{C^2} = {3^2} + {2^2} = 9 + 4 = 13\)
\(AC = \sqrt {13} \) (cm)
Vậy \(AC = BD = \sqrt {13} \)cm; \(AD = BC = \sqrt {10} \) cm
Mục 2 của chương trình Toán 8 Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về đa thức, phân thức đại số. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các công thức, định lý đã học để giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là vô cùng quan trọng để hoàn thành tốt các bài tập này.
Bài tập 1 yêu cầu học sinh thực hiện các phép tính đa thức. Để giải bài tập này, các em cần nắm vững các quy tắc cộng, trừ, nhân, chia đa thức. Ví dụ:
Bài tập 2 yêu cầu học sinh phân tích đa thức thành nhân tử. Để giải bài tập này, các em cần nắm vững các phương pháp phân tích đa thức thành nhân tử như đặt nhân tử chung, sử dụng hằng đẳng thức, nhóm đa thức.
Ví dụ:
Bài tập 3 yêu cầu học sinh rút gọn biểu thức. Để giải bài tập này, các em cần thực hiện các phép toán đa thức, phân thức đại số theo đúng thứ tự ưu tiên. Ví dụ:
(x + 1)/(x - 1) + (x - 1)/(x + 1) = (x2 + 2x + 1 + x2 - 2x + 1)/(x2 - 1) = (2x2 + 2)/(x2 - 1)
Bài tập 4 thường là một bài toán ứng dụng, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết một tình huống thực tế. Để giải bài tập này, các em cần đọc kỹ đề bài, xác định các yếu tố liên quan và xây dựng phương trình hoặc biểu thức toán học phù hợp.
| Công thức | Mô tả |
|---|---|
| (a + b)2 = a2 + 2ab + b2 | Bình phương của một tổng |
| (a - b)2 = a2 - 2ab + b2 | Bình phương của một hiệu |
| a2 - b2 = (a - b)(a + b) | Hiệu hai bình phương |
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 69, 70 SGK Toán 8 Chân trời sáng tạo. Chúc các em học tập tốt!