Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 74 và 75 sách giáo khoa Toán 8 tập 2 – Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập. Hãy cùng theo dõi và tham khảo lời giải nhé!
Cho hai tam giác vuông
Video hướng dẫn giải
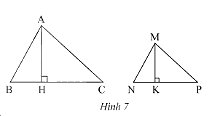
Trong Hình 7, biết \(\Delta MNP\backsim\Delta ABC\) với tỉ số đồng dạng \(k = \frac{{MN}}{{AB}}\), hai đường cao tương ứng là \(MK\) và \(AH\).
a) Chứng minh rằng \(\Delta MNK\backsim\Delta ABH\)và \(\frac{{MK}}{{AH}} = k\).
b) Gọi \({S_1}\) là diện tích tam giác \(MNP\) và \({S_2}\) là diện tích tam giác \(ABC\). Chứng minh rằng \(\frac{{{S_1}}}{{{S_2}}} = {k^2}\).
Phương pháp giải:
- Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
- Diện tích tam giác vuông bằng một nửa tích hai cạnh góc vuông.
Lời giải chi tiết:
a) Vì tam giác \(\Delta MNP\backsim\Delta ABC\) nên \(\widehat B = \widehat N\) (hai góc tương ứng).
Vì \(MK\) là đường cao nên \(\widehat {MKN} = 90^\circ \);Vì \(AH\) là đường cao nên \(\widehat {AHB} = 90^\circ \)
Xét \(\Delta MNK\) và \(\Delta ABH\) có:
\(\widehat B = \widehat N\) (chứng minh trên)
\(\widehat {MKN} = \widehat {AHB} = 90^\circ \)
Do đó, \(\Delta MNK\backsim\Delta ABH\) (g.g)
Vì \(\Delta MNK\backsim\Delta ABH\) nên ta có: \(\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k\).
b) Vì \(\Delta MNP\backsim\Delta ABC\) nên \(\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k\)
\( \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC\)
Vì \(\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH\)
Diện tích tam giác \(MNP\) là:
\({S_1} = \frac{1}{2}.MK.NP\) (đvdt)
Diện tích tam giác \(ABC\) là:
\({S_2} = \frac{1}{2}.AH.BC\) (đvdt)
Ta có: \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}\) (điều phải chứng minh)
Video hướng dẫn giải
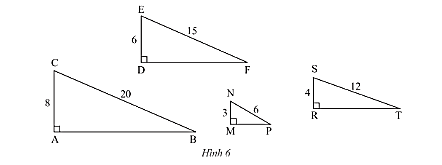
Trong Hình 6, tam giác nào đồng dạng với tam giác \(DEF\)?
Phương pháp giải:
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải chi tiết:
Tỉ số:
\(\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}\).
Xét tam giác\(DEF\) và tam giác\(ABC\) có:
\(\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}\) (chứng minh trên)
Do đó, \(\Delta DEF\backsim\Delta ABC\).
Tỉ số:
\(\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}\).
Vì \(\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}\) nên hai tam giác \(DEF\) và \(MNP\) không đồng dạng với nhau.
Tỉ số:
\(\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}\).
Vì \(\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}\) nên hai tam giác \(DEF\) và \(SRT\) không đồng dạng với nhau.
Video hướng dẫn giải
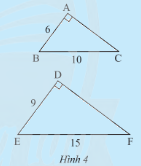
Cho hai tam giác vuông \(ABC\) và \(DEF\) có các kích thước như Hình 4.
a) Hãy tính độ dài cạnh \(AC\) và \(DF\).
b) So sánh các tỉ số \(\frac{{AB}}{{DE}};\frac{{AC}}{{DF}}\) và \(\frac{{BC}}{{EF}}\).
c) Dự đoán sự đồng dạng của hai tam giác\(ABC\) và \(DEF\).
Phương pháp giải:
- Sử dụng định lí Py – ta – go.
- Chứng minh tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh
Lời giải chi tiết:
a) Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} - {6^2} = 64 \Leftrightarrow AC = 8\).
Xét tam giác \(DEF\) vuông tại \(D\) ta có:
\(D{E^2} + D{F^2} = E{F^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} - {9^2} = 144 \Leftrightarrow DF = 12\).
b) Tỉ số:
\(\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}\); \(\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\).
Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\).
c) Xét tam giác\(ABC\) và tam giác\(DEF\) có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta DEF\) (c.c.c)
Video hướng dẫn giải
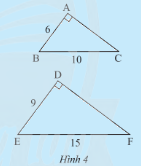
Cho hai tam giác vuông \(ABC\) và \(DEF\) có các kích thước như Hình 4.
a) Hãy tính độ dài cạnh \(AC\) và \(DF\).
b) So sánh các tỉ số \(\frac{{AB}}{{DE}};\frac{{AC}}{{DF}}\) và \(\frac{{BC}}{{EF}}\).
c) Dự đoán sự đồng dạng của hai tam giác\(ABC\) và \(DEF\).
Phương pháp giải:
- Sử dụng định lí Py – ta – go.
- Chứng minh tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh
Lời giải chi tiết:
a) Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} - {6^2} = 64 \Leftrightarrow AC = 8\).
Xét tam giác \(DEF\) vuông tại \(D\) ta có:
\(D{E^2} + D{F^2} = E{F^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} - {9^2} = 144 \Leftrightarrow DF = 12\).
b) Tỉ số:
\(\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}\); \(\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\).
Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\).
c) Xét tam giác\(ABC\) và tam giác\(DEF\) có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta DEF\) (c.c.c)
Video hướng dẫn giải
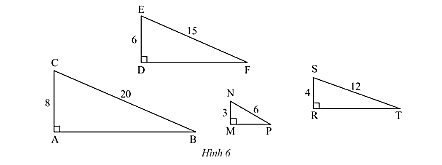
Trong Hình 6, tam giác nào đồng dạng với tam giác \(DEF\)?
Phương pháp giải:
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải chi tiết:
Tỉ số:
\(\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}\).
Xét tam giác\(DEF\) và tam giác\(ABC\) có:
\(\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}\) (chứng minh trên)
Do đó, \(\Delta DEF\backsim\Delta ABC\).
Tỉ số:
\(\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}\).
Vì \(\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}\) nên hai tam giác \(DEF\) và \(MNP\) không đồng dạng với nhau.
Tỉ số:
\(\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}\).
Vì \(\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}\) nên hai tam giác \(DEF\) và \(SRT\) không đồng dạng với nhau.
Video hướng dẫn giải
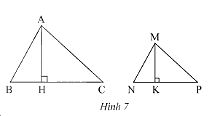
Trong Hình 7, biết \(\Delta MNP\backsim\Delta ABC\) với tỉ số đồng dạng \(k = \frac{{MN}}{{AB}}\), hai đường cao tương ứng là \(MK\) và \(AH\).
a) Chứng minh rằng \(\Delta MNK\backsim\Delta ABH\)và \(\frac{{MK}}{{AH}} = k\).
b) Gọi \({S_1}\) là diện tích tam giác \(MNP\) và \({S_2}\) là diện tích tam giác \(ABC\). Chứng minh rằng \(\frac{{{S_1}}}{{{S_2}}} = {k^2}\).
Phương pháp giải:
- Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
- Diện tích tam giác vuông bằng một nửa tích hai cạnh góc vuông.
Lời giải chi tiết:
a) Vì tam giác \(\Delta MNP\backsim\Delta ABC\) nên \(\widehat B = \widehat N\) (hai góc tương ứng).
Vì \(MK\) là đường cao nên \(\widehat {MKN} = 90^\circ \);Vì \(AH\) là đường cao nên \(\widehat {AHB} = 90^\circ \)
Xét \(\Delta MNK\) và \(\Delta ABH\) có:
\(\widehat B = \widehat N\) (chứng minh trên)
\(\widehat {MKN} = \widehat {AHB} = 90^\circ \)
Do đó, \(\Delta MNK\backsim\Delta ABH\) (g.g)
Vì \(\Delta MNK\backsim\Delta ABH\) nên ta có: \(\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k\).
b) Vì \(\Delta MNP\backsim\Delta ABC\) nên \(\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k\)
\( \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC\)
Vì \(\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH\)
Diện tích tam giác \(MNP\) là:
\({S_1} = \frac{1}{2}.MK.NP\) (đvdt)
Diện tích tam giác \(ABC\) là:
\({S_2} = \frac{1}{2}.AH.BC\) (đvdt)
Ta có: \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}\) (điều phải chứng minh)
Mục 2 của chương trình Toán 8 tập 2 – Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về hình học, đặc biệt là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các định lý, tính chất đã học để chứng minh các mối quan hệ giữa các yếu tố của hình, tính diện tích, chu vi và giải các bài toán thực tế liên quan.
Bài tập này yêu cầu học sinh nhắc lại các định nghĩa, tính chất của hình bình hành, các dấu hiệu nhận biết hình bình hành và vận dụng chúng để giải các bài toán liên quan đến việc chứng minh một tứ giác là hình bình hành, tính độ dài các cạnh, góc của hình bình hành.
Bài tập này tập trung vào việc ôn tập các tính chất của hình chữ nhật, đặc biệt là mối quan hệ giữa đường chéo và các cạnh của hình chữ nhật. Học sinh cần vận dụng các tính chất này để giải các bài toán liên quan đến việc tính độ dài đường chéo, diện tích, chu vi của hình chữ nhật.
Bài tập này yêu cầu học sinh ôn tập các tính chất của hình thoi, đặc biệt là mối quan hệ giữa đường chéo và các cạnh của hình thoi. Học sinh cần vận dụng các tính chất này để giải các bài toán liên quan đến việc tính độ dài đường chéo, diện tích, chu vi của hình thoi.
Bài tập này tập trung vào việc ôn tập các tính chất của hình vuông, bao gồm cả các tính chất của hình chữ nhật và hình thoi. Học sinh cần vận dụng các tính chất này để giải các bài toán liên quan đến việc tính độ dài đường chéo, diện tích, chu vi của hình vuông.
Bài tập: Cho hình bình hành ABCD, có góc A bằng 60 độ. Tính các góc còn lại của hình bình hành.
Lời giải:
Vậy, các góc còn lại của hình bình hành ABCD là: ∠B = 120°, ∠C = 60°, ∠D = 120°.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các trang web học toán online khác. Hãy chủ động tìm kiếm và giải quyết các bài toán khó để nâng cao trình độ của mình.
Hy vọng rằng, với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà chúng tôi đã cung cấp, các em sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 74, 75 SGK Toán 8 tập 2 – Chân trời sáng tạo. Chúc các em học tập tốt!