Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK Toán 8 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Xét cân thăng bằng ở khởi động a) Giải thích tại sao nếu bỏ ra khỏi mỗi đĩa cân một quả cân (x) gam thì cân vẫn thăng bằng. b) Nếu thay quả cân 600 gam bằng quả cân 200 gam (Hình 2) thì cân còn thăng bằng không? Tại sao? c) Tiếp theo, chia các quả cân trên mỗi cân thành ba phần bằng nhau, rồi bỏ ra hai phần (hình 3). Khi đó, cân còn thằng bằng không? Tại sao?
Video hướng dẫn giải
Giải các phương trình sau:
a) \(\dfrac{2}{3}x + 1\dfrac{1}{2} = 0\);
b) \(2\dfrac{1}{2} - 0,75x = 0\).
Phương pháp giải:
Sử dụng các quy tắc:
- Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
Lời giải chi tiết:
a) \(\dfrac{2}{3}x + 1\dfrac{1}{2} = 0\)
\(\dfrac{2}{3}x + \dfrac{3}{2} = 0\)
\(\dfrac{2}{3}x = 0 - \dfrac{3}{2}\) (quy tắc chuyển vế)
\(\dfrac{2}{3}x = \dfrac{{ - 3}}{2}\)
\(x = \dfrac{{ - 3}}{2}:\dfrac{2}{3}\) (quy tắc chia cho một số)
\(x = \dfrac{{ - 9}}{4}\)
Vậy phương trình có nghiệm \(x = \dfrac{{ - 9}}{4}\).
b) \(2\dfrac{1}{2} - 0,75x = 0\)
\(\dfrac{5}{2} - 0,75x = 0\)
\( - 0,75x = 0 - \dfrac{5}{2}\) (quy tắc chuyển vế)
\( - 0,75x = - \dfrac{5}{2}\)
\(x = \left( { - \dfrac{5}{2}} \right):\left( { - 0,75} \right)\) (quy tắc chia cho một số)
\(x = \dfrac{{10}}{3}\)
Vậy phương trình có nghiệm \(x = \dfrac{{10}}{3}\).
Video hướng dẫn giải
Giải các phương trình sau:
a) \(15 - 4x = x - 5\);
b) \(\dfrac{{5x + 2}}{4} + \dfrac{{3x - 2}}{3} = \dfrac{3}{2}\).
Phương pháp giải:
- Quy đồng mẫu số.
- Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
Lời giải chi tiết:
a) \(15 - 4x = x - 5\)
\( - 4x - x = - 5 - 15\) (chuyển vế)
\( - 5x = - 20\)
\(x = \left( { - 20} \right):\left( { - 5} \right)\) (chia cho một số)
\(x = 4\)
Vậy phương trình có nghiệm \(x = 4\).
b) \(\dfrac{{5x + 2}}{4} + \dfrac{{3x - 2}}{3} = \dfrac{3}{2}\)
\(\dfrac{{\left( {5x + 2} \right).3}}{{4.3}} + \dfrac{{\left( {3x - 2} \right).4}}{{3.4}} = \dfrac{{3.6}}{{2.6}}\) (quy đồng mẫu số)
\(\dfrac{{15x + 6}}{{12}} + \dfrac{{12x - 8}}{{12}} = \dfrac{{18}}{{12}}\)
\(15x + 6 + 12x - 8 = 18\) (chia cả hai vế cho một số)
\(15x + 12x = 18 - 6 + 8\) (chuyển vế)
\(27x = 20\) (rút gọn)
\(x = 20:27\) (chia cả hai vế co một số)
\(x = \dfrac{{20}}{{27}}\)
Vậy phương trình có nghiệm \(x = \dfrac{{20}}{{27}}\).
Video hướng dẫn giải
Hai bạn An và Mai giải phương trình \(x = 2x\) như sau:
An: \(x = 2x\)
\(1 = 2\) (chia cả hai vế cho \(x\))
Vậy phương trình vô nghiệm.
Mai: \(x = 2x\)
\(x - 2x = 0\) (chuyển \(2x\) sang vế trái)
\( - x = 0\) (rút gọn)
\(x = 0\) (nhân hai vế với –1)
Vậy phương trình đã cho có nghiệm \(x = 0\).
Em hãy cho biết bạn nào giải đúng.
Phương pháp giải:
Khi chia cả hai vế cho một số thì số đó phải khác 0.
Lời giải chi tiết:
Bạn Mai giải đúng và bạn An giải sai vì khi bạn An chia cả hai vế cho \(x\) thì chưa đảm bảo tính số chia khác 0 do chúng ta chưa biết \(x\).
Video hướng dẫn giải
Xét cân thăng bằng ở khởi động
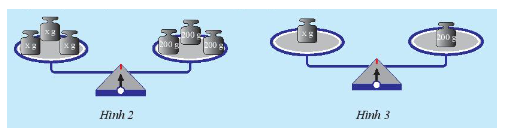
a) Giải thích tại sao nếu bỏ ra khỏi mỗi đĩa cân một quả cân \(x\) gam thì cân vẫn thăng bằng.
b) Nếu thay quả cân 600 gam bằng quả cân 200 gam (Hình 2) thì cân còn thăng bằng không? Tại sao?
c) Tiếp theo, chia các quả cân trên mỗi cân thành ba phần bằng nhau, rồi bỏ ra hai phần (hình 3). Khi đó, cân còn thằng bằng không? Tại sao?
Phương pháp giải:
- Dựa vào quy tắc khi ta cộng hoặc trừ cả hai vế cho một số.
Lời giải chi tiết:
a) Sở dĩ khi bỏ ra khỏi mỗi đĩa cân một quả cân là \(x\) thì cân vẫn thằng bằng vì cả hai bên đĩa cân đều trừ đi một lượng giống nhau là \(x\)gam.
b) Nếu thay quả cân 600 gam bằng qủa cân 200 gam thì cân vẫn cân bằng vì tổng khối lượng 3 quả cân 200 gam là 600 gam.
c) Cân vẫn cân bằng, vì chia đều.
Video hướng dẫn giải
Xét cân thăng bằng ở khởi động
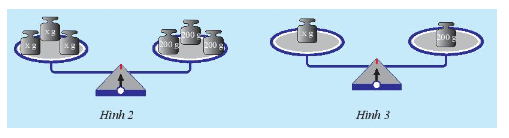
a) Giải thích tại sao nếu bỏ ra khỏi mỗi đĩa cân một quả cân \(x\) gam thì cân vẫn thăng bằng.
b) Nếu thay quả cân 600 gam bằng quả cân 200 gam (Hình 2) thì cân còn thăng bằng không? Tại sao?
c) Tiếp theo, chia các quả cân trên mỗi cân thành ba phần bằng nhau, rồi bỏ ra hai phần (hình 3). Khi đó, cân còn thằng bằng không? Tại sao?
Phương pháp giải:
- Dựa vào quy tắc khi ta cộng hoặc trừ cả hai vế cho một số.
Lời giải chi tiết:
a) Sở dĩ khi bỏ ra khỏi mỗi đĩa cân một quả cân là \(x\) thì cân vẫn thằng bằng vì cả hai bên đĩa cân đều trừ đi một lượng giống nhau là \(x\)gam.
b) Nếu thay quả cân 600 gam bằng qủa cân 200 gam thì cân vẫn cân bằng vì tổng khối lượng 3 quả cân 200 gam là 600 gam.
c) Cân vẫn cân bằng, vì chia đều.
Video hướng dẫn giải
Giải các phương trình sau:
a) \(\dfrac{2}{3}x + 1\dfrac{1}{2} = 0\);
b) \(2\dfrac{1}{2} - 0,75x = 0\).
Phương pháp giải:
Sử dụng các quy tắc:
- Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
Lời giải chi tiết:
a) \(\dfrac{2}{3}x + 1\dfrac{1}{2} = 0\)
\(\dfrac{2}{3}x + \dfrac{3}{2} = 0\)
\(\dfrac{2}{3}x = 0 - \dfrac{3}{2}\) (quy tắc chuyển vế)
\(\dfrac{2}{3}x = \dfrac{{ - 3}}{2}\)
\(x = \dfrac{{ - 3}}{2}:\dfrac{2}{3}\) (quy tắc chia cho một số)
\(x = \dfrac{{ - 9}}{4}\)
Vậy phương trình có nghiệm \(x = \dfrac{{ - 9}}{4}\).
b) \(2\dfrac{1}{2} - 0,75x = 0\)
\(\dfrac{5}{2} - 0,75x = 0\)
\( - 0,75x = 0 - \dfrac{5}{2}\) (quy tắc chuyển vế)
\( - 0,75x = - \dfrac{5}{2}\)
\(x = \left( { - \dfrac{5}{2}} \right):\left( { - 0,75} \right)\) (quy tắc chia cho một số)
\(x = \dfrac{{10}}{3}\)
Vậy phương trình có nghiệm \(x = \dfrac{{10}}{3}\).
Video hướng dẫn giải
Giải các phương trình sau:
a) \(15 - 4x = x - 5\);
b) \(\dfrac{{5x + 2}}{4} + \dfrac{{3x - 2}}{3} = \dfrac{3}{2}\).
Phương pháp giải:
- Quy đồng mẫu số.
- Chuyển một số hạng từ vế bên này sang vế bên kia và đổi dấu số hạng (Quy tắc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
Lời giải chi tiết:
a) \(15 - 4x = x - 5\)
\( - 4x - x = - 5 - 15\) (chuyển vế)
\( - 5x = - 20\)
\(x = \left( { - 20} \right):\left( { - 5} \right)\) (chia cho một số)
\(x = 4\)
Vậy phương trình có nghiệm \(x = 4\).
b) \(\dfrac{{5x + 2}}{4} + \dfrac{{3x - 2}}{3} = \dfrac{3}{2}\)
\(\dfrac{{\left( {5x + 2} \right).3}}{{4.3}} + \dfrac{{\left( {3x - 2} \right).4}}{{3.4}} = \dfrac{{3.6}}{{2.6}}\) (quy đồng mẫu số)
\(\dfrac{{15x + 6}}{{12}} + \dfrac{{12x - 8}}{{12}} = \dfrac{{18}}{{12}}\)
\(15x + 6 + 12x - 8 = 18\) (chia cả hai vế cho một số)
\(15x + 12x = 18 - 6 + 8\) (chuyển vế)
\(27x = 20\) (rút gọn)
\(x = 20:27\) (chia cả hai vế co một số)
\(x = \dfrac{{20}}{{27}}\)
Vậy phương trình có nghiệm \(x = \dfrac{{20}}{{27}}\).
Video hướng dẫn giải
Hai bạn An và Mai giải phương trình \(x = 2x\) như sau:
An: \(x = 2x\)
\(1 = 2\) (chia cả hai vế cho \(x\))
Vậy phương trình vô nghiệm.
Mai: \(x = 2x\)
\(x - 2x = 0\) (chuyển \(2x\) sang vế trái)
\( - x = 0\) (rút gọn)
\(x = 0\) (nhân hai vế với –1)
Vậy phương trình đã cho có nghiệm \(x = 0\).
Em hãy cho biết bạn nào giải đúng.
Phương pháp giải:
Khi chia cả hai vế cho một số thì số đó phải khác 0.
Lời giải chi tiết:
Bạn Mai giải đúng và bạn An giải sai vì khi bạn An chia cả hai vế cho \(x\) thì chưa đảm bảo tính số chia khác 0 do chúng ta chưa biết \(x\).
Mục 2 của chương trình Toán 8 tập 2, Chân trời sáng tạo thường tập trung vào các kiến thức về hình học, cụ thể là các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi, hình vuông. Việc nắm vững các tính chất, dấu hiệu nhận biết và ứng dụng của các tứ giác này là vô cùng quan trọng để giải quyết các bài tập liên quan.
Các bài tập trên trang 32 thường yêu cầu học sinh chứng minh một tứ giác là hình bình hành dựa trên các dấu hiệu nhận biết. Ví dụ:
Lời giải thường dựa trên việc vận dụng các định nghĩa, tính chất của hình bình hành và các định lý liên quan.
Trang 33 tập trung vào việc áp dụng các tính chất của hình bình hành để giải quyết các bài toán về góc, cạnh, đường chéo. Ví dụ:
Cần chú ý sử dụng các tính chất: hai cạnh đối song song và bằng nhau, hai góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Các bài tập trên trang 34 xoay quanh hình chữ nhật, một trường hợp đặc biệt của hình bình hành. Các yêu cầu thường gặp:
Hình chữ nhật có thêm tính chất là bốn góc vuông, do đó cần kết hợp các tính chất của hình bình hành và hình chữ nhật để giải quyết bài toán.
Trang 35 giới thiệu về hình thoi, một trường hợp đặc biệt khác của hình bình hành. Các bài tập thường yêu cầu:
Hình thoi có tính chất đặc biệt là bốn cạnh bằng nhau, cần lưu ý khi giải bài tập.
Khi giải các bài tập về tứ giác, cần phân biệt rõ các loại tứ giác khác nhau và vận dụng đúng các tính chất của từng loại. Ngoài ra, việc vẽ hình chính xác và sử dụng các ký hiệu toán học đúng cách cũng rất quan trọng để trình bày lời giải rõ ràng, dễ hiểu.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 32, 33, 34, 35 SGK Toán 8 tập 2 – Chân trời sáng tạo. Chúc các em học tập tốt!