Chào mừng các em học sinh đến với bài học về Lý thuyết Tính chất đường phân giác của tam giác trong chương trình Toán 8 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về đường phân giác, tính chất của nó và ứng dụng trong giải toán.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các tính chất đặc biệt của đường phân giác, và cách áp dụng những kiến thức này để giải các bài tập thực tế. Hãy cùng bắt đầu nhé!
Đường phân giác của tam giác có tính chất gì?
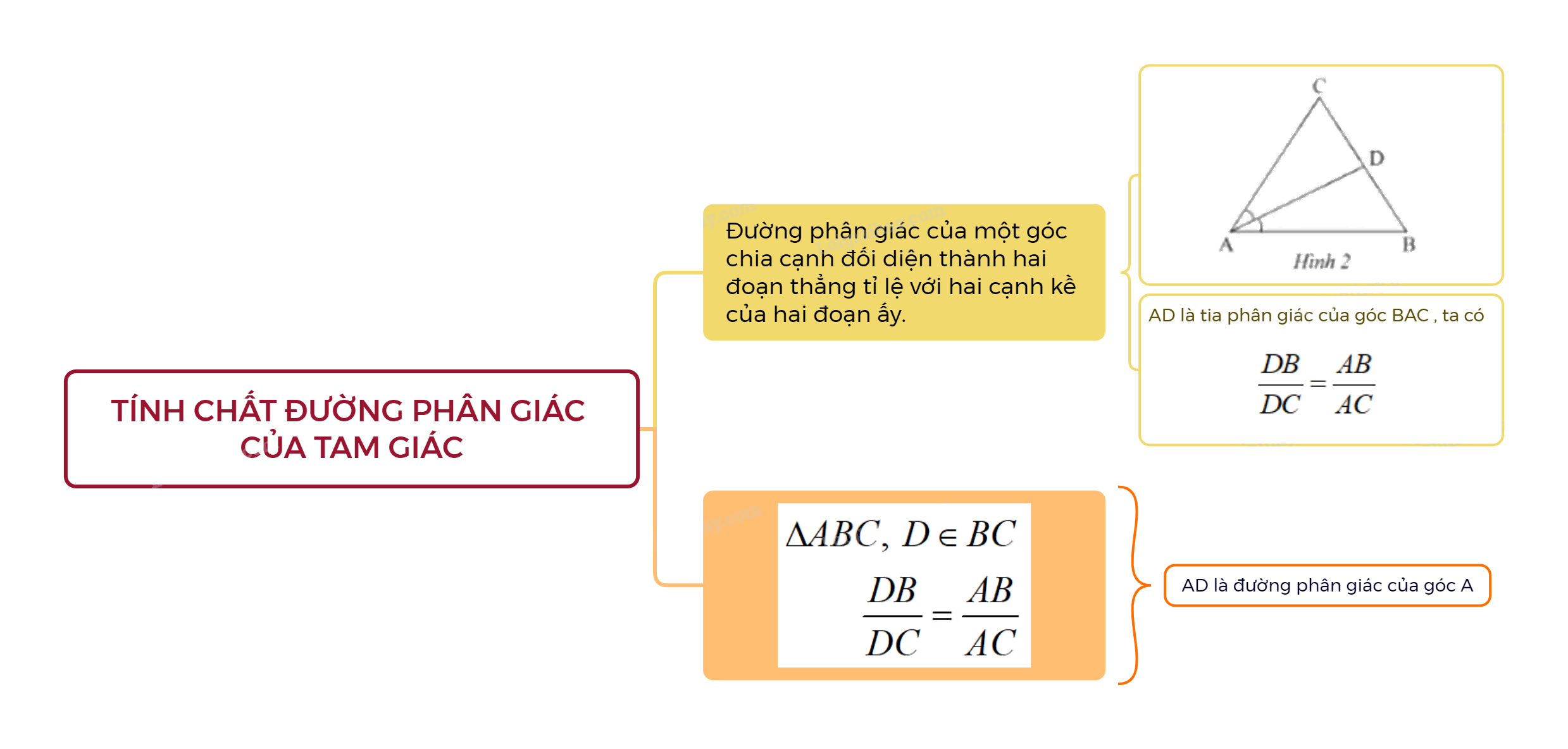
1. Tính chất đường phân giác của tam giác
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.
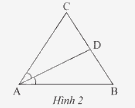
AD là đường phân giác của góc A trong \(\Delta ABC\), \(D \in BC\)
\( \Rightarrow \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\)
Ví dụ:
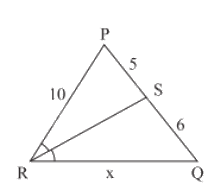
RS là tia phân giác của góc \(\widehat {PRQ}\). Sử dụng tính chất đường phân giác, ta có:
\(\begin{array}{l}\frac{{SQ}}{{SR}} = \frac{{RQ}}{{RP}}\\ \Leftrightarrow \frac{{10}}{5} = \frac{x}{6}\\ \Leftrightarrow 2 = \frac{x}{6}\\ \Leftrightarrow x = 12\end{array}\)
Vậy độ dài đoạn thẳng RQ là 12.
Đường phân giác của một tam giác là đoạn thẳng nối đỉnh của tam giác với điểm chia cạnh đối diện thành hai đoạn thẳng bằng nhau. Trong tam giác ABC, nếu AD là đường phân giác (D thuộc BC) thì BD = CD.
Trong một tam giác, đường phân giác của một góc là tia phân giác của góc đó. Tia phân giác của một góc chia góc đó thành hai góc bằng nhau.
Tính chất quan trọng nhất của đường phân giác là:
Cụ thể, trong tam giác ABC, với AD là đường phân giác (D thuộc BC), ta có:
AB/AC = BD/DC
Tính chất này được sử dụng rộng rãi trong việc giải các bài toán liên quan đến tỉ lệ thức và tam giác đồng dạng.
Ví dụ 1: Cho tam giác ABC có AB = 6cm, AC = 9cm, và AD là đường phân giác (D thuộc BC). Tính BD và DC biết BC = 15cm.
Giải:
Áp dụng tính chất đường phân giác, ta có:
AB/AC = BD/DC
6/9 = BD/DC
BD/DC = 2/3
Mà BD + DC = BC = 15cm
Suy ra BD = (2/5) * 15 = 6cm và DC = (3/5) * 15 = 9cm
Bài tập 1: Cho tam giác MNP có MN = 8cm, MP = 12cm, và NQ là đường phân giác (Q thuộc MP). Tính MQ và QP biết MP = 20cm.
Bài tập 2: Cho tam giác DEF có DE = 5cm, DF = 7cm, và DK là đường phân giác (K thuộc EF). Tính EK và KF biết EF = 12cm.
Ngoài tính chất trên, đường phân giác còn liên quan đến một số khái niệm khác như đường trung tuyến, đường cao. Việc nắm vững mối liên hệ giữa các yếu tố này sẽ giúp các em giải quyết các bài toán phức tạp hơn.
Bài học hôm nay đã cung cấp cho các em những kiến thức cơ bản và quan trọng về Lý thuyết Tính chất đường phân giác của tam giác. Hy vọng rằng, với những kiến thức này, các em sẽ tự tin hơn trong việc giải các bài tập và ứng dụng vào thực tế.
Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và hiểu sâu hơn về chủ đề này nhé!