Chào mừng các em học sinh đến với lời giải chi tiết Bài 6 trang 22 SGK Toán 8 tập 2 – Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, giúp các em học Toán 8 dễ dàng và thú vị hơn. Hãy cùng bắt đầu nhé!
Một người đi bộ trên đường thẳng với tốc độ (vleft( {km/h} right)). Gọi (sleft( {km} right)) là quãng đường đi được trong (tleft( h right)).
a) Lập công thức tính \(s\) theo \(t\).
Phương pháp giải:
- Công thức tính quãng đường: \(s = v.t\)
Lời giải chi tiết:
Cứ 1 giờ người đó lại đi được \(v\) km.
Cứ 2 giờ người đó lại đi được \(2v\)km.
Vậy sau \(t\left( h \right)\) người đó sẽ đi được quãng đường \(v.t\) km.
Vậy ta có công thức tính \(s\)theo \(t\) như sau: \(s = v.t\) trong đó \(v\) là vận tốc, \(t\) là thời gian và \(s\) là quãng đường đi được.
Video hướng dẫn giải
Một người đi bộ trên đường thẳng với tốc độ \(v\left( {km/h} \right)\). Gọi \(s\left( {km} \right)\) là quãng đường đi được trong \(t\left( h \right)\).
a) Lập công thức tính \(s\) theo \(t\).
Phương pháp giải:
- Công thức tính quãng đường: \(s = v.t\)
Lời giải chi tiết:
Cứ 1 giờ người đó lại đi được \(v\) km.
Cứ 2 giờ người đó lại đi được \(2v\)km.
Vậy sau \(t\left( h \right)\) người đó sẽ đi được quãng đường \(v.t\) km.
Vậy ta có công thức tính \(s\)theo \(t\) như sau: \(s = v.t\) trong đó \(v\) là vận tốc, \(t\) là thời gian và \(s\) là quãng đường đi được.
b) Vẽ đồ thị của hàm số \(s\) theo \(t\) khi \(v = 4\).
Phương pháp giải:
- Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\). Đồ thị hàm số \(y = ax\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
Lời giải chi tiết:
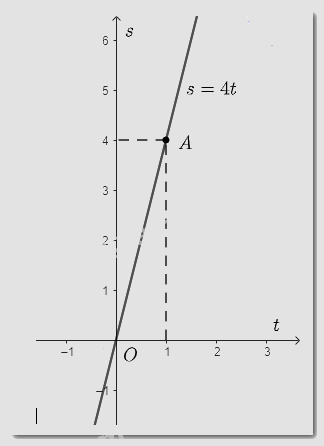
Với \(v = 4 \Rightarrow s = 4t\). Khi đó \(s\) là hàm số bậc nhất theo biến \(t\).
Với \(t = 1 \Rightarrow s = 4.1 = 4 \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;4} \right)\).
Đồ thị hàm số \(s = 4t\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;4} \right)\).
b) Vẽ đồ thị của hàm số \(s\) theo \(t\) khi \(v = 4\).
Phương pháp giải:
- Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\). Đồ thị hàm số \(y = ax\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
Lời giải chi tiết:
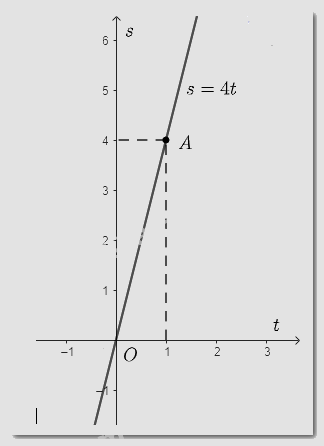
Với \(v = 4 \Rightarrow s = 4t\). Khi đó \(s\) là hàm số bậc nhất theo biến \(t\).
Với \(t = 1 \Rightarrow s = 4.1 = 4 \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;4} \right)\).
Đồ thị hàm số \(s = 4t\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;4} \right)\).
Bài 6 trang 22 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức đã học về hình học, cụ thể là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các định lý, định nghĩa và biết cách áp dụng chúng vào việc chứng minh các tính chất hình học.
Bài 6 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Hình bình hành là tứ giác có các cặp cạnh đối song song. Các tính chất của hình bình hành bao gồm:
Để chứng minh một tứ giác là hình bình hành, ta có thể sử dụng một trong các cách sau:
Hình chữ nhật là hình bình hành có một góc vuông. Các tính chất của hình chữ nhật bao gồm:
Hình thoi là hình bình hành có bốn cạnh bằng nhau. Các tính chất của hình thoi bao gồm:
Hình vuông là hình bình hành có bốn cạnh bằng nhau và một góc vuông. Các tính chất của hình vuông bao gồm:
Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Chứng minh rằng DE là đường phân giác của góc ADC.
Giải:
Bài 6 trang 22 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về các hình học và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.