Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 31, 32 SGK Toán 8 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập trong mục này tập trung vào các kiến thức cơ bản về số thực, phép toán trên số thực và ứng dụng của chúng.
Một hình chữ nhật lớn được ghép bởi hai hình chữ nhật A và B lần lượt có diện tích là (a) (c{m^2}) và có cùng chiều dài (x) cm (Hình 1). a) Tính chiều rộng của hình chữ nhật lớn theo hai cách khác nhau. b) Chiều rộng của B lớn hơn chiều rộng của A bao nhiêu? Biết (b > a)
Video hướng dẫn giải
Thực hiện các phép tính cộng, trừ phân thức sau:
a) \(\dfrac{x}{{x + 3}} + \dfrac{{2 - x}}{{x + 3}}\)
b) \(\dfrac{{{x^2}y}}{{x - y}} - \dfrac{{x{y^2}}}{{x - y}}\)
c) \(\dfrac{{2x}}{{2x - y}} + \dfrac{y}{{y - 2x}}\)
Phương pháp giải:
a) b) Sử dụng quy tắc cộng, trừ hai phân thức có cùng mẫu số
c) Biến đổi hai phân thức thành hai phân thức có cùng mẫu số rồi sử dụng quy tắc cộng, trừ hai phân thức có cùng mẫu số.
Lời giải chi tiết:
a) ĐKXĐ: \(x \ne - 3\)
\(\dfrac{x}{{x + 3}} + \dfrac{{2 - x}}{{x + 3}}\)\( = \dfrac{{x + 2 - x}}{{x + 3}} = \dfrac{2}{{x + 3}}\)
b) ĐKXĐ: \(x \ne y\)
\(\dfrac{{{x^2}y}}{{x - y}} - \dfrac{{x{y^2}}}{{x - y}}\)\( = \dfrac{{{x^2}y - x{y^2}}}{{x - y}} = \dfrac{{xy\left( {x - y} \right)}}{{x - y}} = xy\)
c) ĐKXĐ: \(2x \ne y\)
\(\dfrac{{2x}}{{2x - y}} + \dfrac{y}{{y - 2x}}\) \( = \dfrac{{2x}}{{2x - y}} - \dfrac{y}{{2x - y}} = \dfrac{{2x - y}}{{2x - y}} = 1\)
Video hướng dẫn giải
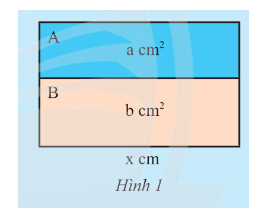
Một hình chữ nhật lớn được ghép bởi hai hình chữ nhật A và B lần lượt có diện tích là \(a\) \(c{m^2}\) và có cùng chiều dài \(x\) cm (Hình 1).
a) Tính chiều rộng của hình chữ nhật lớn theo hai cách khác nhau.
b) Chiều rộng của B lớn hơn chiều rộng của A bao nhiêu? Biết \(b > a\)
Phương pháp giải:
a) Sử dụng kiến thức: Chiều rộng hình chữ nhật bằng diện tích chia cho chiều dài
b) Tính hiệu chiều rộng của hình B và hình A
Lời giải chi tiết:
a) Cách 1: Chiều rộng hình chữ nhật lớn là: \(\left( {a + b} \right):x = \dfrac{{a + b}}{x}\) (cm)
Cách 2: Chiều rộng của hình chữ nhật A là: \(a:x = \dfrac{a}{x}\) (cm)
Chiều rộng của hình chữ nhật B là: \(b:x = \dfrac{b}{x}\) (cm)
Chiều rộng của hình chữ nhật lớn là: \(\dfrac{a}{x} + \dfrac{b}{x} = \dfrac{{a + b}}{x}\) (cm)
b) Chiều rộng của B lớn hơn chiều rộng của A là: \(\dfrac{a}{x} - \dfrac{b}{x} = \dfrac{{a - b}}{x}\) (cm)
Video hướng dẫn giải
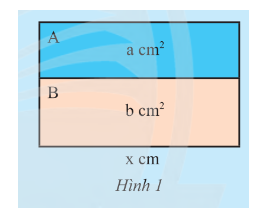
Một hình chữ nhật lớn được ghép bởi hai hình chữ nhật A và B lần lượt có diện tích là \(a\) \(c{m^2}\) và có cùng chiều dài \(x\) cm (Hình 1).
a) Tính chiều rộng của hình chữ nhật lớn theo hai cách khác nhau.
b) Chiều rộng của B lớn hơn chiều rộng của A bao nhiêu? Biết \(b > a\)
Phương pháp giải:
a) Sử dụng kiến thức: Chiều rộng hình chữ nhật bằng diện tích chia cho chiều dài
b) Tính hiệu chiều rộng của hình B và hình A
Lời giải chi tiết:
a) Cách 1: Chiều rộng hình chữ nhật lớn là: \(\left( {a + b} \right):x = \dfrac{{a + b}}{x}\) (cm)
Cách 2: Chiều rộng của hình chữ nhật A là: \(a:x = \dfrac{a}{x}\) (cm)
Chiều rộng của hình chữ nhật B là: \(b:x = \dfrac{b}{x}\) (cm)
Chiều rộng của hình chữ nhật lớn là: \(\dfrac{a}{x} + \dfrac{b}{x} = \dfrac{{a + b}}{x}\) (cm)
b) Chiều rộng của B lớn hơn chiều rộng của A là: \(\dfrac{a}{x} - \dfrac{b}{x} = \dfrac{{a - b}}{x}\) (cm)
Video hướng dẫn giải
Thực hiện các phép tính cộng, trừ phân thức sau:
a) \(\dfrac{x}{{x + 3}} + \dfrac{{2 - x}}{{x + 3}}\)
b) \(\dfrac{{{x^2}y}}{{x - y}} - \dfrac{{x{y^2}}}{{x - y}}\)
c) \(\dfrac{{2x}}{{2x - y}} + \dfrac{y}{{y - 2x}}\)
Phương pháp giải:
a) b) Sử dụng quy tắc cộng, trừ hai phân thức có cùng mẫu số
c) Biến đổi hai phân thức thành hai phân thức có cùng mẫu số rồi sử dụng quy tắc cộng, trừ hai phân thức có cùng mẫu số.
Lời giải chi tiết:
a) ĐKXĐ: \(x \ne - 3\)
\(\dfrac{x}{{x + 3}} + \dfrac{{2 - x}}{{x + 3}}\)\( = \dfrac{{x + 2 - x}}{{x + 3}} = \dfrac{2}{{x + 3}}\)
b) ĐKXĐ: \(x \ne y\)
\(\dfrac{{{x^2}y}}{{x - y}} - \dfrac{{x{y^2}}}{{x - y}}\)\( = \dfrac{{{x^2}y - x{y^2}}}{{x - y}} = \dfrac{{xy\left( {x - y} \right)}}{{x - y}} = xy\)
c) ĐKXĐ: \(2x \ne y\)
\(\dfrac{{2x}}{{2x - y}} + \dfrac{y}{{y - 2x}}\) \( = \dfrac{{2x}}{{2x - y}} - \dfrac{y}{{2x - y}} = \dfrac{{2x - y}}{{2x - y}} = 1\)
Mục 1 của SGK Toán 8 tập 1 chương trình Chân trời sáng tạo giới thiệu về các khái niệm cơ bản của số thực, bao gồm số hữu tỉ, số vô tỉ, và cách biểu diễn chúng trên trục số. Các bài tập trong mục này yêu cầu học sinh vận dụng kiến thức về số thực để thực hiện các phép toán cộng, trừ, nhân, chia, và so sánh các số thực.
Bài 1 tập trung vào việc củng cố khái niệm về số thực. Học sinh cần phân biệt được số hữu tỉ và số vô tỉ, biết cách biểu diễn chúng trên trục số, và hiểu được mối quan hệ giữa các loại số này.
Bài 2 giới thiệu về các phép toán cộng, trừ, nhân, chia trên số thực. Học sinh cần nắm vững các quy tắc thực hiện các phép toán này, và biết cách áp dụng chúng để giải các bài tập cụ thể.
Để giải các bài tập trong mục 1 trang 31, 32 SGK Toán 8 tập 1 chương trình Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Ví dụ 1: Tính giá trị của biểu thức: 2,5 + (-3,7) - 1,2
Giải:
2,5 + (-3,7) - 1,2 = (2,5 - 3,7) - 1,2 = -1,2 - 1,2 = -2,4
Để củng cố kiến thức về số thực và các phép toán trên số thực, học sinh có thể thực hiện thêm các bài tập sau:
Mục 1 trang 31, 32 SGK Toán 8 tập 1 chương trình Chân trời sáng tạo là một phần quan trọng trong chương trình học Toán 8. Việc nắm vững kiến thức và kỹ năng trong mục này sẽ giúp học sinh có nền tảng vững chắc để học các kiến thức tiếp theo. Hy vọng rằng, với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ học tập tốt môn Toán và đạt được kết quả cao.