Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho từng bài tập trong SGK Toán 8 tập 2, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 8 tập 2 tập trung vào các kiến thức quan trọng về hình học và đại số. Việc giải đúng các bài tập trong mục này là nền tảng vững chắc cho các kiến thức nâng cao hơn.
Trên một tờ giấy kẻ cảo có các đường kẻ ngang song song và cách đều nhau
Video hướng dẫn giải
Với số liệu đo đạc được ghi trên Hình 14, hãy tính bề rộng \(CD\) của con kênh.
Phương pháp giải:
Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Vì \(\widehat {ABE} = \widehat {ACD} \Rightarrow BE//CD\) (hai góc đồng vị bằng nhau)
Trong tam giác \(ACD\) có \(BE//CD\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}}\) mà \(AC = AB + BC = 8 + 8 = 16\)
Suy ra, \(\frac{8}{{16}} = \frac{3}{{CD}} \Rightarrow CD = \frac{{3.16}}{8} = 6\).
Vậy bề rộng \(CD\) của con sông là 6m.
Video hướng dẫn giải
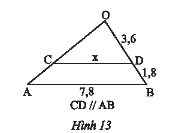
Tìm độ dài \(x\) trên Hình 13.
Phương pháp giải:
Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Trong tam giác \(OAB\) có \(CD//AB\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OD}}{{OB}} = \frac{{CD}}{{AB}}\) mà \(OB = OD + DB = 3,6 + 1,8 = 5,4\)
Suy ra, \(\frac{{3,6}}{{5,4}} = \frac{x}{{7,8}} \Rightarrow x = \frac{{3,6.7,8}}{{5,4}} = 5,2\).
Vậy \(x = 5,2\).
Video hướng dẫn giải
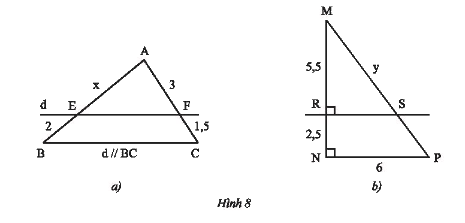
Tính độ dài \(x;y\) trong Hình 8.
Phương pháp giải:
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
a)
Xét tam giác \(ABC\) có \(d//BC\) mà \(d\) cắt \(AB;AC\) lần lượt tại \(E\) và \(F\)nên theo định lí Thales ta có:
\(\frac{{AE}}{{BE}} = \frac{{AF}}{{CF}} \Rightarrow \frac{x}{2} = \frac{3}{{1,5}}\). Do đó, \(x = \frac{{2.3}}{{1,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MN = NR + MR = 2,5 + 5,5 = 8\)
Xét tam giác \(MNP\) vuông tại \(N\) ta có:
\(M{N^2} + N{P^2} = M{P^2}\)
\({8^2} + {6^2} = M{P^2}\)
\(100 = M{P^2} \Rightarrow MP = \sqrt {100} = 10\)
Xét tam giác \(MNP\) có \(\left\{ \begin{array}{l}RS \bot MN\\NP \bot MN\end{array} \right. \Rightarrow RS//NP\) (quan hệ từ vuông góc đến song song) nên theo định lí Thales ta có:
\(\frac{{MR}}{{MN}} = \frac{{MS}}{{MP}} \Rightarrow \frac{{5,5}}{8} = \frac{y}{{10}}\). Do đó, \(y = \frac{{5,5.10}}{8} = 6,875\).
Vậy \(y = 6,875\).
Video hướng dẫn giải
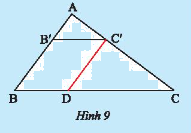
Cho tam giác \(ABC\) có \(AB = 6cm,AC = 8cm\) và \(BC = 10cm\). Lấy điểm \(B'\) trên \(AB\) sao cho AB' = 2cm. Qua \(B'\) vẽ đường thẳng song song với \(BC\) và cắt \(AC\) tại \(C'\).
a) Tính \(AC'\).
b) Qua \(C'\) vẽ đường thẳng song song với \(AB\) và cắt \(BC\) tại \(D\). Tính \(BD,B'C'\).
c) Tính và so sánh các tỉ số: \(\frac{{AB'}}{{AB}},\frac{{AC'}}{{AC}}\) và \(\frac{{B'C'}}{{BC}}\).
Phương pháp giải:
- Sử dụng Định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
- Hình bình hành có các cặp cạnh đối song song và bằng nhau.
Lời giải chi tiết:
a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).
Vậy \(AC' = \frac{{16}}{3}cm\).
b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:
\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).
Vậy \(BD = \frac{{10}}{3}cm\).
Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)
Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))
Xét tứ giác \(B'C'DB\) có
\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)
c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
Video hướng dẫn giải
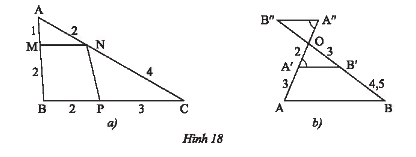
Hãy chỉ ra các cặp đường thẳng song song với nhau trong mỗi hình dưới đây.
Phương pháp giải:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết:
a) \(AB = AM + MB = 1 + 2 = 3;AC = AN + NC = 2 + 4 = 6;BC = BP + PC = 2 + 3 = 5\)
Ta có: \(\frac{{AM}}{{AB}} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{2}{6} = \frac{1}{3}\).
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{3}\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(MN//BC\).
Ta có: \(\frac{{CN}}{{CA}} = \frac{4}{6} = \frac{2}{3};\frac{{CP}}{{CB}} = \frac{3}{5}\).
Vì \(\frac{{CN}}{{AC}} \ne \frac{{CP}}{{BC}}\left( {\frac{2}{3} \ne \frac{3}{5}} \right)\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(NP\) không song song với \(BC\).
b) Vì \(\widehat {B''A''O} = \widehat {OA'B'}\) mà hai góc này ở vị trí so le trong nên \(A''B''//A'B'\).
\(OA = OA' + A'A = 2 + 3 = 5;OB = OB' + B'B = 3 + 4,5 = 7,5\)
Ta có: \(\frac{{OA'}}{{OA}} = \frac{2}{5};\frac{{OB'}}{{OB}} = \frac{3}{{7,5}} = \frac{2}{5}\).
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{2}{5}\) nên theo định lí Thales đảo trong tam giác \(OAB\), ta có \(A'B'//AB\).
Vì \(\left\{ \begin{array}{l}A'B'//AB\\A'B'//A''B''\end{array} \right. \Rightarrow AB//A''B''\).
Video hướng dẫn giải
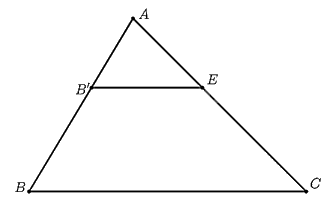
Cho tam giác \(ABC\) có \(AB = 6cm,AC = 15cm\). Trên \(AB,AC\) lần lượt lấy \(B',C'\) sao cho \(AB' = 2cm;AC' = 5cm\).
a) Tính các tỉ số \(\frac{{AB'}}{{AB}}\) và \(\frac{{AC'}}{{AC}}\).
b) Qua \(B'\) vẽ đường thẳng song song với \(BC\) cắt \(AC\) tại \(E\). Tính \(AE\).
c) So sánh \(AE\) và \(AC'\).
d) Hãy nhận xét về vị trí của \(E\) và \(C'\), vị trí của hai đường thẳng \(B'C'\) và \(B'E\).
Phương pháp giải:
- Sử dụng Định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
a) Ta có:
\(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3}\) và \(\frac{{AC'}}{{AC}} = \frac{5}{{15}} = \frac{1}{3}\).
b) Vì \(B'E//BC\) và\(B'E\) cắt \(AC\) tại \(E\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AE}}{{15}} \Rightarrow AE = \frac{{2.15}}{6} = 5cm\)
c) Ta có: \(AE = AC' = 5cm\).
d) Điểm \(E \equiv C'\) và đường thẳng \(B'C' \equiv B'E\).
Video hướng dẫn giải
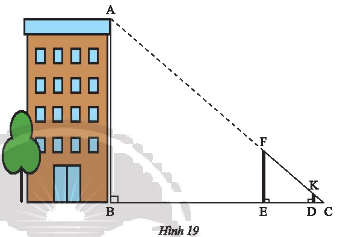
Đo chiều cao \(AB\) của một tòa nhà bằng hai cây cọc \(FE,DK\), một sợi dây và một thước cuộn như sau:
- Đặt cọc \(FE\) cố định, di chuyển cọc \(DK\) sao cho nhìn thấy \(K,F,A\) thẳng hàng.
- Căng thẳng dây \(FC\) đi qua \(K\) và cắt mặt đất tại \(C\).
- Đo khoảng cách \(BC\) và \(DC\) trên mặt đất.
Cho biết \(DK = 1m,BC = 24m,DC = 1,2m\). Tính chiều cao \(AB\) của tòa nhà.
Phương pháp giải:
Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Vì \(\left\{ \begin{array}{l}KD \bot BC\\AB \bot BC\end{array} \right. \Rightarrow KD//AB\).
Xét tam giác \(CAB\) có \(KD//AB \Rightarrow \frac{{KD}}{{AB}} = \frac{{DC}}{{BC}}\) (hệ quả của định lí Thales).
\( \Rightarrow \frac{1}{{AB}} = \frac{{1,2}}{{24}} \Rightarrow AB = \frac{{24.1}}{{1,2}} = 20m\)
Vậy chiều cao \(AB\) của tòa nhà là 20m.
Video hướng dẫn giải
Trên một tờ giấy kẻ caro có các đường kẻ ngang song song và cách đều nhau.
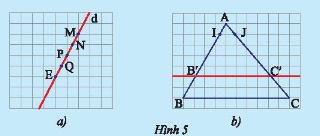
a) Vẽ một đường thẳng \(d\) cắt các đường kẻ ngang của tờ giấy như trong Hình 5a. Hãy so sánh độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\).
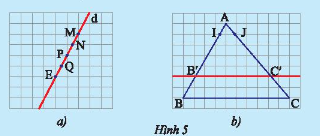
b) Vẽ một tam giác \(ABC\) rồi vẽ một đường thẳng song song với cạnh \(BC\) và cắt hai cạnh \(AB,AC\) lần lượt tại \(B'\) và \(C'\). Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo tính tỉ số \(AB'\) và \(BB'\); trên cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo tính tỉ số \(AC'\) và \(C'C\) (Hình 5b).
So sánh các tỉ số \(\frac{{AB'}}{{AB}}\) và \(\frac{{AC'}}{{AC}}\);\(\frac{{AB'}}{{B'B}}\) và \(\frac{{AC'}}{{C'C}}\);\(\frac{{B'B}}{{AB}}\) và \(\frac{{C'C}}{{AC}}\).
Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
a) Quan sát hình vẽ ta thấy độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\) đều bằng nhau.
b) Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo nên độ dài \(AB' = 5AI;BB' = 2AI;\) Trên \(AB = 7AI\); cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo nên độ dài \(AC' = 5AJ;C'C = 2AJ\);\(AC = 7AJ\).
Tỉ số \(AB'\) và \(B'B\) là \(AB':B'B = \frac{{AB'}}{{B'B}} = \frac{{5AI}}{{2AI}} = \frac{5}{2}\);
Tỉ số \(AC'\) và \(C'C\) là \(AC':C'C = \frac{{AC'}}{{C'C}} = \frac{{5AJ}}{{2AJ}} = \frac{5}{2}\).
Do đó, \(\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}} = \frac{5}{2}\).
Ta có: \(\frac{{AB'}}{{AB}} = \frac{{5AI}}{{7AI}} = \frac{5}{7};\frac{{AC'}}{{AC}} = \frac{{5AJ}}{{7AJ}} = \frac{5}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{5}{7}\).
Ta có: \(\frac{{B'B}}{{AB}} = \frac{{2AI}}{{7AI}} = \frac{2}{7};\frac{{C'C}}{{AC}} = \frac{{2AJ}}{{7AJ}} = \frac{2}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{2}{7}\).
Video hướng dẫn giải
Trên một tờ giấy kẻ caro có các đường kẻ ngang song song và cách đều nhau.
a) Vẽ một đường thẳng \(d\) cắt các đường kẻ ngang của tờ giấy như trong Hình 5a. Hãy so sánh độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\).
b) Vẽ một tam giác \(ABC\) rồi vẽ một đường thẳng song song với cạnh \(BC\) và cắt hai cạnh \(AB,AC\) lần lượt tại \(B'\) và \(C'\). Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo tính tỉ số \(AB'\) và \(BB'\); trên cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo tính tỉ số \(AC'\) và \(C'C\) (Hình 5b).
So sánh các tỉ số \(\frac{{AB'}}{{AB}}\) và \(\frac{{AC'}}{{AC}}\);\(\frac{{AB'}}{{B'B}}\) và \(\frac{{AC'}}{{C'C}}\);\(\frac{{B'B}}{{AB}}\) và \(\frac{{C'C}}{{AC}}\).
Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
a) Quan sát hình vẽ ta thấy độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\) đều bằng nhau.
b) Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo nên độ dài \(AB' = 5AI;BB' = 2AI;\) Trên \(AB = 7AI\); cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo nên độ dài \(AC' = 5AJ;C'C = 2AJ\);\(AC = 7AJ\).
Tỉ số \(AB'\) và \(B'B\) là \(AB':B'B = \frac{{AB'}}{{B'B}} = \frac{{5AI}}{{2AI}} = \frac{5}{2}\);
Tỉ số \(AC'\) và \(C'C\) là \(AC':C'C = \frac{{AC'}}{{C'C}} = \frac{{5AJ}}{{2AJ}} = \frac{5}{2}\).
Do đó, \(\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}} = \frac{5}{2}\).
Ta có: \(\frac{{AB'}}{{AB}} = \frac{{5AI}}{{7AI}} = \frac{5}{7};\frac{{AC'}}{{AC}} = \frac{{5AJ}}{{7AJ}} = \frac{5}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{5}{7}\).
Ta có: \(\frac{{B'B}}{{AB}} = \frac{{2AI}}{{7AI}} = \frac{2}{7};\frac{{C'C}}{{AC}} = \frac{{2AJ}}{{7AJ}} = \frac{2}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{2}{7}\).
Video hướng dẫn giải
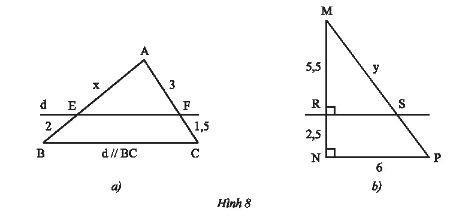
Tính độ dài \(x;y\) trong Hình 8.
Phương pháp giải:
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
a)
Xét tam giác \(ABC\) có \(d//BC\) mà \(d\) cắt \(AB;AC\) lần lượt tại \(E\) và \(F\)nên theo định lí Thales ta có:
\(\frac{{AE}}{{BE}} = \frac{{AF}}{{CF}} \Rightarrow \frac{x}{2} = \frac{3}{{1,5}}\). Do đó, \(x = \frac{{2.3}}{{1,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MN = NR + MR = 2,5 + 5,5 = 8\)
Xét tam giác \(MNP\) vuông tại \(N\) ta có:
\(M{N^2} + N{P^2} = M{P^2}\)
\({8^2} + {6^2} = M{P^2}\)
\(100 = M{P^2} \Rightarrow MP = \sqrt {100} = 10\)
Xét tam giác \(MNP\) có \(\left\{ \begin{array}{l}RS \bot MN\\NP \bot MN\end{array} \right. \Rightarrow RS//NP\) (quan hệ từ vuông góc đến song song) nên theo định lí Thales ta có:
\(\frac{{MR}}{{MN}} = \frac{{MS}}{{MP}} \Rightarrow \frac{{5,5}}{8} = \frac{y}{{10}}\). Do đó, \(y = \frac{{5,5.10}}{8} = 6,875\).
Vậy \(y = 6,875\).
Video hướng dẫn giải
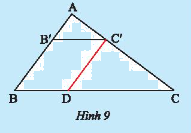
Cho tam giác \(ABC\) có \(AB = 6cm,AC = 8cm\) và \(BC = 10cm\). Lấy điểm \(B'\) trên \(AB\) sao cho AB' = 2cm. Qua \(B'\) vẽ đường thẳng song song với \(BC\) và cắt \(AC\) tại \(C'\).
a) Tính \(AC'\).
b) Qua \(C'\) vẽ đường thẳng song song với \(AB\) và cắt \(BC\) tại \(D\). Tính \(BD,B'C'\).
c) Tính và so sánh các tỉ số: \(\frac{{AB'}}{{AB}},\frac{{AC'}}{{AC}}\) và \(\frac{{B'C'}}{{BC}}\).
Phương pháp giải:
- Sử dụng Định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
- Hình bình hành có các cặp cạnh đối song song và bằng nhau.
Lời giải chi tiết:
a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).
Vậy \(AC' = \frac{{16}}{3}cm\).
b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:
\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).
Vậy \(BD = \frac{{10}}{3}cm\).
Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)
Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))
Xét tứ giác \(B'C'DB\) có
\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)
c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
Video hướng dẫn giải
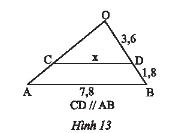
Tìm độ dài \(x\) trên Hình 13.
Phương pháp giải:
Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Trong tam giác \(OAB\) có \(CD//AB\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OD}}{{OB}} = \frac{{CD}}{{AB}}\) mà \(OB = OD + DB = 3,6 + 1,8 = 5,4\)
Suy ra, \(\frac{{3,6}}{{5,4}} = \frac{x}{{7,8}} \Rightarrow x = \frac{{3,6.7,8}}{{5,4}} = 5,2\).
Vậy \(x = 5,2\).
Video hướng dẫn giải
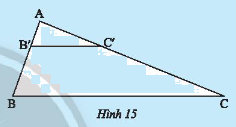
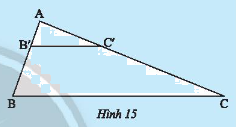
Với số liệu đo đạc được ghi trên Hình 14, hãy tính bề rộng \(CD\) của con kênh.
Phương pháp giải:
Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Vì \(\widehat {ABE} = \widehat {ACD} \Rightarrow BE//CD\) (hai góc đồng vị bằng nhau)
Trong tam giác \(ACD\) có \(BE//CD\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}}\) mà \(AC = AB + BC = 8 + 8 = 16\)
Suy ra, \(\frac{8}{{16}} = \frac{3}{{CD}} \Rightarrow CD = \frac{{3.16}}{8} = 6\).
Vậy bề rộng \(CD\) của con sông là 6m.
Video hướng dẫn giải
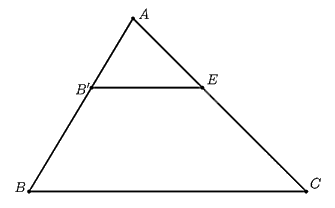
Cho tam giác \(ABC\) có \(AB = 6cm,AC = 15cm\). Trên \(AB,AC\) lần lượt lấy \(B',C'\) sao cho \(AB' = 2cm;AC' = 5cm\).
a) Tính các tỉ số \(\frac{{AB'}}{{AB}}\) và \(\frac{{AC'}}{{AC}}\).
b) Qua \(B'\) vẽ đường thẳng song song với \(BC\) cắt \(AC\) tại \(E\). Tính \(AE\).
c) So sánh \(AE\) và \(AC'\).
d) Hãy nhận xét về vị trí của \(E\) và \(C'\), vị trí của hai đường thẳng \(B'C'\) và \(B'E\).
Phương pháp giải:
- Sử dụng Định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
a) Ta có:
\(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3}\) và \(\frac{{AC'}}{{AC}} = \frac{5}{{15}} = \frac{1}{3}\).
b) Vì \(B'E//BC\) và\(B'E\) cắt \(AC\) tại \(E\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AE}}{{15}} \Rightarrow AE = \frac{{2.15}}{6} = 5cm\)
c) Ta có: \(AE = AC' = 5cm\).
d) Điểm \(E \equiv C'\) và đường thẳng \(B'C' \equiv B'E\).
Video hướng dẫn giải
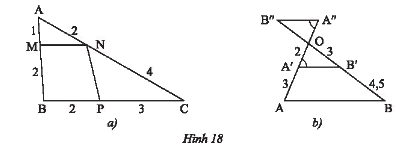
Hãy chỉ ra các cặp đường thẳng song song với nhau trong mỗi hình dưới đây.
Phương pháp giải:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết:
a) \(AB = AM + MB = 1 + 2 = 3;AC = AN + NC = 2 + 4 = 6;BC = BP + PC = 2 + 3 = 5\)
Ta có: \(\frac{{AM}}{{AB}} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{2}{6} = \frac{1}{3}\).
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{3}\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(MN//BC\).
Ta có: \(\frac{{CN}}{{CA}} = \frac{4}{6} = \frac{2}{3};\frac{{CP}}{{CB}} = \frac{3}{5}\).
Vì \(\frac{{CN}}{{AC}} \ne \frac{{CP}}{{BC}}\left( {\frac{2}{3} \ne \frac{3}{5}} \right)\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(NP\) không song song với \(BC\).
b) Vì \(\widehat {B''A''O} = \widehat {OA'B'}\) mà hai góc này ở vị trí so le trong nên \(A''B''//A'B'\).
\(OA = OA' + A'A = 2 + 3 = 5;OB = OB' + B'B = 3 + 4,5 = 7,5\)
Ta có: \(\frac{{OA'}}{{OA}} = \frac{2}{5};\frac{{OB'}}{{OB}} = \frac{3}{{7,5}} = \frac{2}{5}\).
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{2}{5}\) nên theo định lí Thales đảo trong tam giác \(OAB\), ta có \(A'B'//AB\).
Vì \(\left\{ \begin{array}{l}A'B'//AB\\A'B'//A''B''\end{array} \right. \Rightarrow AB//A''B''\).
Video hướng dẫn giải
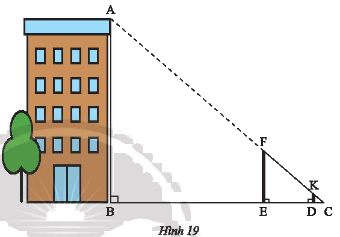
Đo chiều cao \(AB\) của một tòa nhà bằng hai cây cọc \(FE,DK\), một sợi dây và một thước cuộn như sau:
- Đặt cọc \(FE\) cố định, di chuyển cọc \(DK\) sao cho nhìn thấy \(K,F,A\) thẳng hàng.
- Căng thẳng dây \(FC\) đi qua \(K\) và cắt mặt đất tại \(C\).
- Đo khoảng cách \(BC\) và \(DC\) trên mặt đất.
Cho biết \(DK = 1m,BC = 24m,DC = 1,2m\). Tính chiều cao \(AB\) của tòa nhà.
Phương pháp giải:
Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Vì \(\left\{ \begin{array}{l}KD \bot BC\\AB \bot BC\end{array} \right. \Rightarrow KD//AB\).
Xét tam giác \(CAB\) có \(KD//AB \Rightarrow \frac{{KD}}{{AB}} = \frac{{DC}}{{BC}}\) (hệ quả của định lí Thales).
\( \Rightarrow \frac{1}{{AB}} = \frac{{1,2}}{{24}} \Rightarrow AB = \frac{{24.1}}{{1,2}} = 20m\)
Vậy chiều cao \(AB\) của tòa nhà là 20m.
Mục 2 trong SGK Toán 8 tập 2 – Chân trời sáng tạo thường bao gồm các bài tập liên quan đến các kiến thức đã học trong chương. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững lý thuyết, hiểu rõ các định nghĩa, tính chất và định lý liên quan. Đồng thời, việc luyện tập thường xuyên với các bài tập đa dạng sẽ giúp củng cố kiến thức và rèn luyện kỹ năng giải toán.
Mục 2 thường bao gồm các nội dung sau:
Các bài tập trang 46 thường tập trung vào việc ôn tập các kiến thức cơ bản về hình học. Ví dụ, bài tập yêu cầu học sinh xác định các yếu tố của hình tam giác, tính góc, tính độ dài cạnh. Để giải các bài tập này, học sinh cần nhớ lại các định nghĩa, tính chất và định lý liên quan đến tam giác.
Trang 47 thường chứa các bài tập về tứ giác. Học sinh cần nắm vững các tính chất của các loại tứ giác khác nhau (hình vuông, hình chữ nhật, hình thoi, hình bình hành) để giải quyết các bài tập này. Ngoài ra, học sinh cũng cần biết cách sử dụng các định lý về tứ giác để chứng minh các tính chất hình học.
Các bài tập trang 48 thường liên quan đến các bài toán về đường thẳng song song và đường thẳng vuông góc. Học sinh cần nắm vững các dấu hiệu nhận biết đường thẳng song song, đường thẳng vuông góc và các tính chất của chúng để giải quyết các bài tập này.
Trang 49 thường chứa các bài tập về phương trình bậc nhất một ẩn. Học sinh cần nắm vững các bước giải phương trình bậc nhất một ẩn và các quy tắc biến đổi phương trình để giải quyết các bài tập này. Ngoài ra, học sinh cũng cần biết cách kiểm tra lại nghiệm của phương trình.
Để học tập hiệu quả môn Toán 8, học sinh cần:
Giaitoan.edu.vn hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả này, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 8 và đạt được kết quả tốt nhất.