Bài 9 trang 59 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9 trang 59 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho
Đề bài
Cho \(\Delta ABC\) biết \(AM\) là đường phân giác. Trong các khẳng định sau, khẳng định nào đúng?
A. \(\frac{{BM}}{{MC}} = \frac{{AB}}{{AC}}\).
B. \(\frac{{AB}}{{MC}} = \frac{{BM}}{{AC}}\).
C. \(\frac{{AM}}{{MC}} = \frac{{AB}}{{AC}}\).
D. \(\frac{{BM}}{{MC}} = \frac{{AM}}{{AC}}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng Tính chất đường phân giác trong tam giác:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
Lời giải chi tiết
Chọn đáp án A
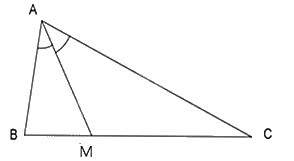
Vì \(AM\) là tia phân giác góc \(A\left( {M \in BC} \right)\) nên theo tính chất đường phân giác ta có:
\(\frac{{BM}}{{CM}} = \frac{{AB}}{{AC}};\frac{{BM}}{{AB}} = \frac{{CM}}{{AC}};\frac{{CM}}{{BM}} = \frac{{AC}}{{AB}};\frac{{AC}}{{CM}} = \frac{{AB}}{{BM}}\).
Bài 9 trang 59 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số, đặc biệt là các quy tắc cộng, trừ, nhân, chia đa thức để giải quyết bài toán. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như đơn thức, đa thức, bậc của đa thức, hệ số của đa thức, và các phép toán trên đa thức.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Xác định rõ các đại lượng đã cho và đại lượng cần tìm. Phân tích mối quan hệ giữa các đại lượng này để tìm ra phương pháp giải phù hợp.
Đề bài: (Giả sử đề bài là: Phân tích các đa thức sau thành nhân tử: a) x2 - 4; b) x2 + 4x + 4; c) x3 - 8)
Áp dụng công thức hiệu hai bình phương: a2 - b2 = (a - b)(a + b)
x2 - 4 = x2 - 22 = (x - 2)(x + 2)
Nhận thấy x2 + 4x + 4 là một bình phương của một tổng: (a + b)2 = a2 + 2ab + b2
x2 + 4x + 4 = x2 + 2.x.2 + 22 = (x + 2)2
Áp dụng công thức hiệu hai lập phương: a3 - b3 = (a - b)(a2 + ab + b2)
x3 - 8 = x3 - 23 = (x - 2)(x2 + 2x + 4)
Ngoài bài 9 trang 59, SGK Toán 8 tập 2 – Chân trời sáng tạo còn có nhiều bài tập tương tự yêu cầu học sinh phân tích đa thức thành nhân tử. Các dạng bài tập này thường bao gồm:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức về các phép toán trên đa thức, các hằng đẳng thức đáng nhớ, và các phương pháp phân tích đa thức thành nhân tử.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh nên làm thêm các bài tập tương tự trong sách bài tập, đề thi thử, hoặc các trang web học toán online. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin giải các bài tập khó hơn.
Bài 9 trang 59 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về bài tập này và tự tin giải các bài tập tương tự.