Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 59, 60 SGK Toán 8 Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập trong mục này tập trung vào các kiến thức quan trọng của chương trình Toán 8, đòi hỏi các em phải vận dụng linh hoạt các định lý, công thức đã học.
Vẽ vào vở tam giác (ABC)
Video hướng dẫn giải
Tìm tam giác vuông trong các tam giác sau:
a) Tam giác \(EFK\) có \(EF = 9\)m, \(FK = 12\)m, \(EK = 15\)m.
b) Tam giác \(PQR\) có \(PQ = 17\)cm, \(QR = 12\)cm, \(PR = 10\)cm.
c) Tam giác \(DEF\) có \(DE = 8\)m, \(DF = 6\)m, \(EF = 10\)m.
Phương pháp giải:
Sử dụng định lý Pythagore đảo để tìm các tam giác vuông.
Lời giải chi tiết:
a) Ta có: \({9^2} + {12^2} = {15^2}\), suy ra \(E{F^2} + F{K^2} = E{K^2}\). Vậy tam giác \(EFK\) vuông tại \(F\)
b) Ta có cạnh \(PQ\) là cạnh dài nhất và \({12^2} + {15^2} \ne {17^2}\), suy ra \(Q{R^2} + P{R^2} \ne P{Q^2}\). Vậy tam giác \(PQR\) không phải là tam giác vuông
c) Ta có: \({8^2} + {6^2} = {10^2}\), suy ra \(D{E^2} + D{F^2} = E{F^2}\). Vậy tam giác \(DEF\) vuông tại \(D\)
Video hướng dẫn giải
a) Nam dự định làm một cái êke từ ba thanh nẹp gỗ. Nam đã có hai thanh làm hai cạnh góc vuông dài \(6\)cm và \(8\)cm. Hỏi thanh nẹp còn lại Nam phải làm có độ dài bao nhiêu? (Giả sử các mối nối không đáng kể).
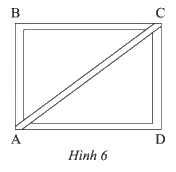
b) Một khung gỗ \(ABCD\) (Hình 6) được tạo thành từ \(5\) thanh nẹp có độ dài như sau: \(AB = CD = 36\)cm; \(BC = AD = 48\)cm; \(AC = 60\)cm. Chứng minh rằng \(\widehat {ABC}\) và \(\widehat {ADC}\) là các góc vuông.
Phương pháp giải:
a) Sử dụng định lý Pythagore tính độ dài cạnh còn lại
b) Sử dụng định lý Pythagore đảo chứng minh \(\Delta ABC\), \(\Delta ADC\) là các tam giác vuông
Lời giải chi tiết:
a) Gọi \(a\), \(b\) là độ dài hai thanh nẹp làm cạnh góc vuông (cm)
Gọi \(c\) là độ dài thanh nẹp còn lại cần tính (cm)
Áp dụng định lý Pythagore ta có:
\({c^2} = {a^2} + {b^2}\)
\({c^2} = {6^2} + {8^2} = 36 + 64 = 100 = {10^2}\)
\(c = 10\) (cm)
Vậy độ dài thanh nẹp còn lại là \(10\)cm
b) Ta có: \({60^2} = {36^2} + {48^2}\)
Suy ra \(A{C^2} = A{B^2} + B{C^2}\) và \(A{C^2} = A{D^2} + C{D^2}\)
Suy ra \(\Delta ABC\) vuông tại \(B\), \(\Delta ACD\) vuông tại \(D\)
\(\widehat {ABC} = 90^\circ ;\;\widehat {ADC} = 90^\circ \)
Video hướng dẫn giải
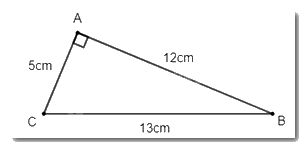
Vẽ vào vở tam giác \(ABC\) có \(AB = 12\)cm, \(AC = 5\)cm, \(BC = 13\)cm, rồi xác định số đo \(\widehat {BAC}\) bằng thước đo góc.
Phương pháp giải:
Vẽ tam giác theo đúng số đo độ dài rồi sử dụng thước đo góc xác định số đo của góc \(\widehat {BAC}\)
Lời giải chi tiết:
- Vẽ hình theo yêu cầu ta thu được hình dưới đây:
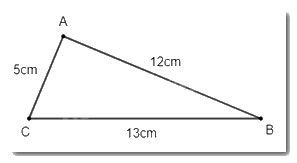
- Tiến hành đo góc, ta xác định được \(\widehat {BAC} = 90^\circ \)\(\)
Video hướng dẫn giải
Vẽ vào vở tam giác \(ABC\) có \(AB = 12\)cm, \(AC = 5\)cm, \(BC = 13\)cm, rồi xác định số đo \(\widehat {BAC}\) bằng thước đo góc.
Phương pháp giải:
Vẽ tam giác theo đúng số đo độ dài rồi sử dụng thước đo góc xác định số đo của góc \(\widehat {BAC}\)
Lời giải chi tiết:
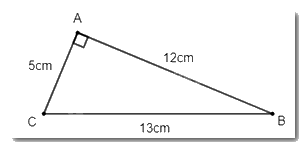
- Vẽ hình theo yêu cầu ta thu được hình dưới đây:
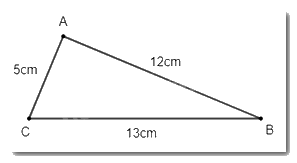
- Tiến hành đo góc, ta xác định được \(\widehat {BAC} = 90^\circ \)\(\)
Video hướng dẫn giải
Tìm tam giác vuông trong các tam giác sau:
a) Tam giác \(EFK\) có \(EF = 9\)m, \(FK = 12\)m, \(EK = 15\)m.
b) Tam giác \(PQR\) có \(PQ = 17\)cm, \(QR = 12\)cm, \(PR = 10\)cm.
c) Tam giác \(DEF\) có \(DE = 8\)m, \(DF = 6\)m, \(EF = 10\)m.
Phương pháp giải:
Sử dụng định lý Pythagore đảo để tìm các tam giác vuông.
Lời giải chi tiết:
a) Ta có: \({9^2} + {12^2} = {15^2}\), suy ra \(E{F^2} + F{K^2} = E{K^2}\). Vậy tam giác \(EFK\) vuông tại \(F\)
b) Ta có cạnh \(PQ\) là cạnh dài nhất và \({12^2} + {15^2} \ne {17^2}\), suy ra \(Q{R^2} + P{R^2} \ne P{Q^2}\). Vậy tam giác \(PQR\) không phải là tam giác vuông
c) Ta có: \({8^2} + {6^2} = {10^2}\), suy ra \(D{E^2} + D{F^2} = E{F^2}\). Vậy tam giác \(DEF\) vuông tại \(D\)
Video hướng dẫn giải
a) Nam dự định làm một cái êke từ ba thanh nẹp gỗ. Nam đã có hai thanh làm hai cạnh góc vuông dài \(6\)cm và \(8\)cm. Hỏi thanh nẹp còn lại Nam phải làm có độ dài bao nhiêu? (Giả sử các mối nối không đáng kể).
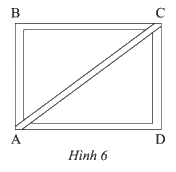
b) Một khung gỗ \(ABCD\) (Hình 6) được tạo thành từ \(5\) thanh nẹp có độ dài như sau: \(AB = CD = 36\)cm; \(BC = AD = 48\)cm; \(AC = 60\)cm. Chứng minh rằng \(\widehat {ABC}\) và \(\widehat {ADC}\) là các góc vuông.
Phương pháp giải:
a) Sử dụng định lý Pythagore tính độ dài cạnh còn lại
b) Sử dụng định lý Pythagore đảo chứng minh \(\Delta ABC\), \(\Delta ADC\) là các tam giác vuông
Lời giải chi tiết:
a) Gọi \(a\), \(b\) là độ dài hai thanh nẹp làm cạnh góc vuông (cm)
Gọi \(c\) là độ dài thanh nẹp còn lại cần tính (cm)
Áp dụng định lý Pythagore ta có:
\({c^2} = {a^2} + {b^2}\)
\({c^2} = {6^2} + {8^2} = 36 + 64 = 100 = {10^2}\)
\(c = 10\) (cm)
Vậy độ dài thanh nẹp còn lại là \(10\)cm
b) Ta có: \({60^2} = {36^2} + {48^2}\)
Suy ra \(A{C^2} = A{B^2} + B{C^2}\) và \(A{C^2} = A{D^2} + C{D^2}\)
Suy ra \(\Delta ABC\) vuông tại \(B\), \(\Delta ACD\) vuông tại \(D\)
\(\widehat {ABC} = 90^\circ ;\;\widehat {ADC} = 90^\circ \)
Mục 2 trang 59, 60 SGK Toán 8 Chân trời sáng tạo thường xoay quanh các chủ đề về hình học, cụ thể là các định lý liên quan đến tứ giác, hình thang cân, và các tính chất của đường trung bình trong tam giác, hình thang. Việc nắm vững các định lý này là nền tảng để giải quyết các bài tập một cách hiệu quả.
Để giải các bài tập trong mục 2 trang 59, 60 SGK Toán 8 Chân trời sáng tạo, các em cần thực hiện theo các bước sau:
Bài tập: Cho hình thang cân ABCD (AB // CD), AB = 6cm, CD = 10cm, AD = 5cm. Tính độ dài đường trung bình của hình thang.
Giải:
Đường trung bình của hình thang ABCD là MN, với M là trung điểm của AD và N là trung điểm của BC.
Theo tính chất của đường trung bình hình thang, ta có:
MN = (AB + CD) / 2 = (6 + 10) / 2 = 8cm
Vậy, độ dài đường trung bình của hình thang ABCD là 8cm.
Trong mục 2 trang 59, 60 SGK Toán 8 Chân trời sáng tạo, các em có thể gặp các dạng bài tập sau:
Để giải nhanh các bài tập trong mục 2, các em có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em nên luyện tập thêm các bài tập tương tự trong sách bài tập, đề thi thử và các nguồn tài liệu học tập khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán khó.
Hy vọng với những hướng dẫn chi tiết này, các em sẽ giải quyết thành công các bài tập trong mục 2 trang 59, 60 SGK Toán 8 Chân trời sáng tạo. Chúc các em học tập tốt!