Chào mừng các em học sinh đến với lời giải chi tiết Bài 2 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, giúp các em học Toán 8 dễ dàng và thú vị hơn. Hãy cùng bắt đầu với lời giải Bài 2 trang 14 nhé!
Vẽ một hệ trục tọa độ (Oxy) và đánh dấu các điểm
Đề bài
Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm \(M\left( {0;-2} \right);N\left( {0;1} \right);P\left( {0;4} \right)\).
a) Em có nhận xét gì về các điểm \(M;N;P\)?
b) Em hãy cho biết một điểm bất kì trên trục tung có hoành độ bằng bao nhiêu.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Điểm \(A\left( {{x_0};{y_0}} \right)\) thì hoành độ là \({x_0}\) và tung độ là \({y_0}\).
- Điểm \(B\left( {0;b} \right)\) nằm trên trục tung, tung độ là \(b\).
- Điểm \(C\left( {c;0} \right)\) nằm trên trục hoành, hoành độ là \(c\).
Lời giải chi tiết
Điểm \(M\left( {0; - 2} \right) \Rightarrow \) hoành độ là 0 và tung độ là -2.
Điểm \(N\left( {0;1} \right) \Rightarrow \) hoành độ là 0 và tung độ là 1.
Điểm \(P\left( {0;4} \right) \Rightarrow \) hoành độ là 0 và tung độ là 4.
Biểu diễn ba điểm \(M;N;P\) trên hệ trục tọa độ ta được
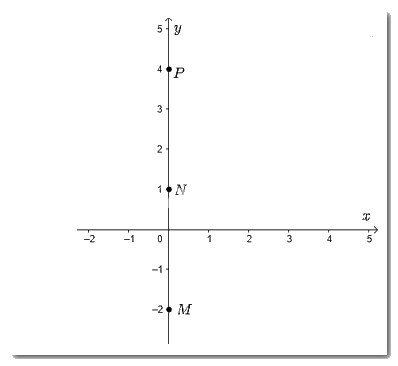
Nhận xét: Cả ba điểm \(M;N;P\) đều nằm trên trục tung.
b) Từ ví dụ ở câu a ta thấy tất cả các điểm nằm trên trục tung đều có hoành độ bằng 0.
Bài 2 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc ôn tập và củng cố kiến thức về các phép toán cơ bản, các tính chất của số thực, và ứng dụng trong giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để thực hiện các phép tính, so sánh và sắp xếp các số thực.
Bài 2 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giải Bài 2 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo một cách hiệu quả, các em cần:
Ví dụ 1: Tính giá trị của biểu thức: 2,5 + (-3,7) - 1,2
Giải:
2,5 + (-3,7) - 1,2 = (2,5 - 3,7) - 1,2 = -1,2 - 1,2 = -2,4
Ví dụ 2: So sánh hai số thực: -2,5 và -3,1
Giải:
-2,5 > -3,1 (vì -2,5 lớn hơn -3,1 trên trục số)
Khi thực hiện các phép tính với số thực, các em cần chú ý đến dấu của các số và áp dụng đúng các quy tắc. Ngoài ra, việc kiểm tra lại kết quả sau khi tính toán là rất quan trọng để đảm bảo tính chính xác.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tự giải thêm các bài tập tương tự sau:
Bài 2 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp các em ôn tập và củng cố kiến thức về số thực và các phép toán cơ bản. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em sẽ hiểu bài và làm bài tập một cách hiệu quả. Chúc các em học tốt!
| Số thực | Giá trị tuyệt đối |
|---|---|
| 2,5 | 2,5 |
| -3,7 | 3,7 |
| 0 | 0 |
| Bảng giá trị tuyệt đối của một số số thực | |