Chào mừng các em học sinh đến với bài học về lý thuyết Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều trong chương trình Toán 8 - Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về các khái niệm này.
Chúng ta sẽ cùng nhau tìm hiểu về cách tính diện tích xung quanh, diện tích đáy và thể tích của hai loại hình chóp phổ biến này. Đồng thời, bài học cũng sẽ giúp các em nắm vững các công thức và áp dụng chúng vào giải các bài tập thực tế.
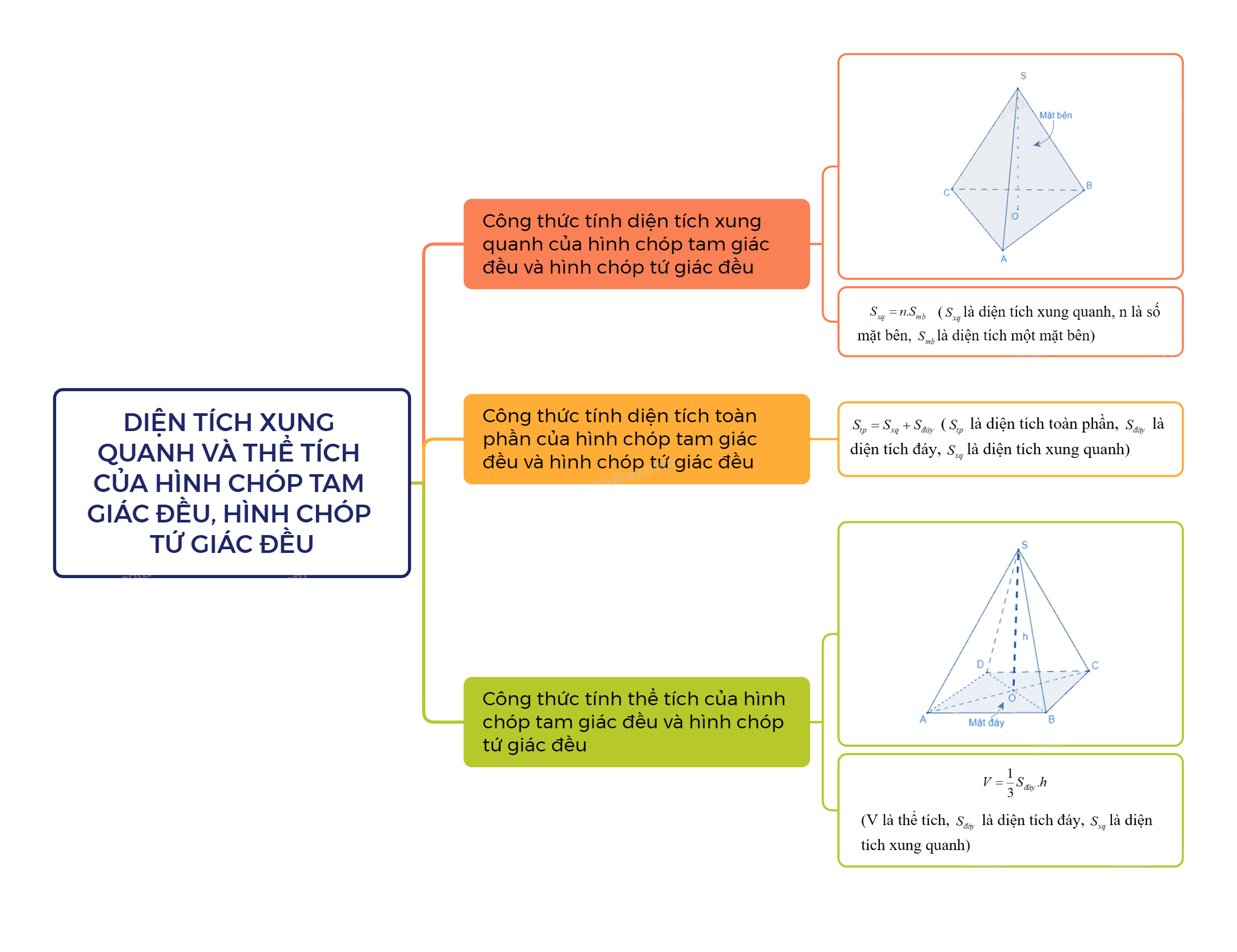
Công thức tính diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều
Công thức tính diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều
Diện tích xung quanh của hình chóp tam giác đều (hình chóp tứ giác đều) bằng tổng diện tích của các mặt bên.
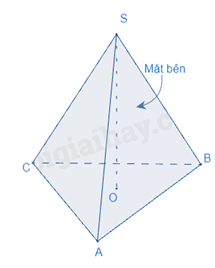
Diện tích toàn phần của hình chóp tam giác đều (hình chóp tứ giác đều) bằng tổng của diện tích xung quanh và diện tích đáy: (\({S_{tp}} = {S_{xq}} + {S_{đáy}}\) (\({S_{tp}}\) là diện tích toàn phần, là diện tích đáy, \({S_{xq}}\) là diện tích xung quanh)
Công thức tính thể tích của hình chóp tam giác đều và hình chóp tứ giác đều
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng \(\frac{1}{3}\) diện tích đáy nhân với chiều cao.
\(V = \frac{1}{3}{S_{đáy}}.h\).
(V là thể tích, \({S_{đáy}}\) là diện tích đáy, \(h\) là chiều cao)
Ví dụ:
Cho hình chóp tứ giác đều sau:
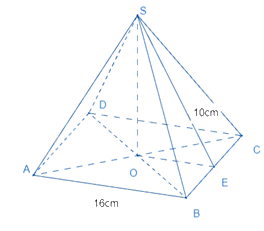
Diện tích xung quanh của hình chóp là: \({S_{xq}} = 4.\frac{1}{2}.10.16 = 320(c{m^2})\)
Diện tích toàn phần của hình chóp là: \[{S_{tp}} = {S_{xq}} + {S_{đáy}} = 320 + 16.16 = 576(c{m^2})\]
Chiều cao của hình chóp là: \(\sqrt {{{10}^2} - {{\left( {\frac{{16}}{2}} \right)}^2}} = \sqrt {100 - 64} = \sqrt {36} = 6(cm)\)
Thể tích của hình chóp là: \(V = \frac{1}{3}.6.16.16 = 512(c{m^3})\)
Trong chương trình Toán 8, kiến thức về hình học không gian đóng vai trò quan trọng, và hình chóp là một trong những hình cơ bản cần nắm vững. Bài viết này sẽ đi sâu vào lý thuyết về diện tích xung quanh và thể tích của hình chóp tam giác đều và hình chóp tứ giác đều, theo chương trình SGK Toán 8 - Chân trời sáng tạo.
Hình chóp là hình đa diện có một mặt đáy là đa giác và các mặt bên là các tam giác có chung đỉnh. Đỉnh chung đó gọi là đỉnh của hình chóp. Chiều cao của hình chóp là khoảng cách từ đỉnh đến mặt đáy.
Hình chóp tam giác đều: Là hình chóp có đáy là tam giác đều và các mặt bên là các tam giác cân bằng nhau.
Hình chóp tứ giác đều: Là hình chóp có đáy là hình vuông và các mặt bên là các tam giác cân bằng nhau.
Diện tích xung quanh của hình chóp được tính bằng tổng diện tích của các mặt bên.
Trong đó:
Diện tích đáy của hình chóp được tính tùy thuộc vào hình dạng của đa giác đáy.
Thể tích của hình chóp được tính theo công thức:
Thể tích = (1/3) * Diện tích đáy * Chiều cao
Trong đó:
Bài 1: Tính diện tích xung quanh và thể tích của hình chóp tam giác đều có cạnh đáy là 5cm và chiều cao mặt bên là 4cm.
Giải:
Bài 2: Tính thể tích của hình chóp tứ giác đều có cạnh đáy là 6cm và chiều cao là 8cm.
Giải:
Khi giải các bài toán liên quan đến hình chóp, cần chú ý:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức cần thiết về lý thuyết Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều. Chúc các em học tập tốt!
| Hình chóp | Diện tích xung quanh | Thể tích |
|---|---|---|
| Tam giác đều | 3 * (1/2 * cạnh đáy * chiều cao mặt bên) | (1/3) * Diện tích đáy * Chiều cao |
| Tứ giác đều | 4 * (1/2 * cạnh đáy * chiều cao mặt bên) | (1/3) * Diện tích đáy * Chiều cao |