Chào mừng bạn đến với bài học lý thuyết Tứ giác trong chương trình Toán 8 - Chân trời sáng tạo tại giaitoan.edu.vn. Bài viết này sẽ cung cấp đầy đủ kiến thức nền tảng, định nghĩa, tính chất và các dạng bài tập thường gặp về tứ giác.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập hiệu quả với nội dung được trình bày rõ ràng, dễ hiểu, kèm theo nhiều ví dụ minh họa và bài tập thực hành.
Tứ giác là gì?
1. Khái niệm
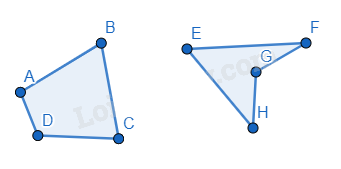
Tứ giác ABCD là một hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Ví dụ:
- Đặc điểm
+Có 4 đỉnh
+ Có 4 cạnh
Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.
Ví dụ: ABCD là tứ giác lồi, EFGH không phải là tứ giác lồi.
2. Tính chất
+Hai cạnh kề nhau là hai cạnh chung đỉnh.
+ Hai cạnh kề nhau tạo thành góc của tứ giác.
+ Hai cạnh đối nhau không chung đỉnh.
+ Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.
+ Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
3. Định lí tổng các góc của một tứ giác
Tổng số đo các góc của một tứ giác bằng \({360^0}\).
Tứ giác ABCD, \(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\)
Ví dụ:
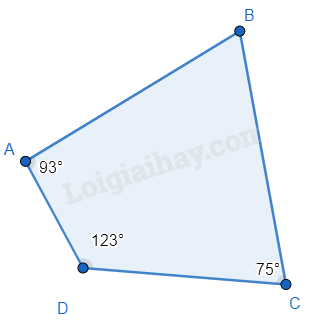
\(\widehat B = {360^0} - {93^0} - {123^0} - {75^0} = {69^0}\)
Tứ giác là một trong những khái niệm cơ bản và quan trọng trong hình học lớp 8. Việc nắm vững lý thuyết về tứ giác không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho việc học các kiến thức hình học nâng cao hơn.
Tứ giác là hình có bốn cạnh và bốn góc. Bốn đỉnh của tứ giác là bốn điểm bất kỳ trên mặt phẳng, không có ba điểm nào thẳng hàng. Ký hiệu tứ giác ABCD được viết theo thứ tự các đỉnh.
Tổng các góc trong một tứ giác luôn bằng 360 độ. Điều này có thể được chứng minh bằng cách chia tứ giác thành hai tam giác.
Dưới đây là một số bài tập vận dụng để giúp bạn hiểu rõ hơn về lý thuyết tứ giác:
Ngoài các kiến thức cơ bản về tứ giác, bạn có thể tìm hiểu thêm về các khái niệm liên quan như đường trung bình của tam giác, đường trung tuyến của tam giác, và các định lý về tứ giác nội tiếp đường tròn.
Lý thuyết tứ giác là một phần quan trọng trong chương trình Toán 8. Hy vọng rằng bài viết này đã cung cấp cho bạn đầy đủ kiến thức và kỹ năng cần thiết để giải quyết các bài tập về tứ giác một cách hiệu quả. Chúc bạn học tập tốt!