Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 8 Chân trời sáng tạo, đặc biệt là mục 3 trang 18, 19, 20, 21.
Mục tiêu của chúng tôi là giúp các em học tập hiệu quả, nắm vững kiến thức và tự tin giải quyết các bài toán Toán 8.
Hùng mua (x) mét dây điện và phải trả số tiền là (y) nghìn đồng. Giá trị tương ứng giữa (x)và (y) được cho bởi bảng sau:
Video hướng dẫn giải
Một lò xo có chiều dài ban đầu khi chưa treo vật nặng là 10 cm. Cho biết treo thêm vào lò xo 1 vật nặng 1 kg thì chiều dài lò xo tăng thêm 3 cm.
a) Tính chiều dài \(y\) (cm) của lò xo theo khối lượng \(x\) (kg) của vật.
b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).
Phương pháp giải:
Độ dài của lò xo sau khi treo vật nặng bằng độ dài ban đầu của lò xo cộng với độ dài tăng thêm do bị ảnh hưởng của vật nặng.
Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\).
Lời giải chi tiết:
Vì cứ treo thêm 1 kg vật nặng thì lò xo dài thêm 3 cm nên treo thêm \(x\) kg vật nặng thì lò xo dài thêm \(3x\) cm.
Chiều dài của lò xo sau khi treo vật nặng là:
\(y = 3x + 10\).
b) Vẽ đồ thị hàm số \(y = 3x + 10\)
Cho \(x = 0 \Rightarrow y = 10\) ta được điểm \(M\left( {0;10} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 10}}{3}\) ta được điểm \(N\left( {\dfrac{{ - 10}}{3};0} \right)\) trên \(Ox\).
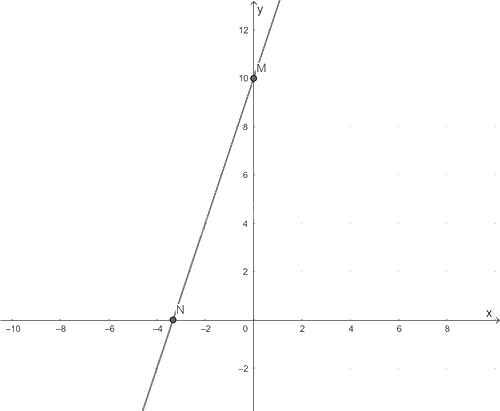
Đồ thị hàm số \(y = 3x + 10\) là đường thẳng đi qua hai điểm \(M;N\).
Video hướng dẫn giải
Vẽ đồ thị của các hàm số sau:
a) \(y = 5x + 2\);
b) \(y = - 2x - 6\);
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\).
Lời giải chi tiết:
a) \(y = 5x + 2\);
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{5}\) ta được điểm \(B\left( {\dfrac{{ - 2}}{5};0} \right)\) trên \(Ox\).
Vẽ đường thẳng đi qua hai điểm \(A;B\) ta được đồ thị của hàm số \(y = 5x + 2\).
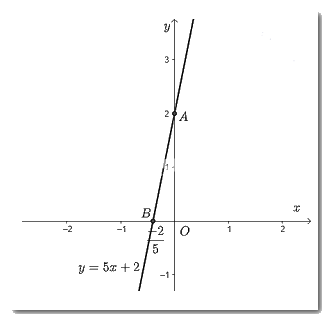
b) \(y = - 2x - 6\)
Cho \(x = 0 \Rightarrow y = - 6\) ta được điểm \(C\left( {0; - 6} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = - 3\) ta được điểm \(D\left( { - 3;0} \right)\) trên \(Ox\).
Vẽ đường thẳng đi qua hai điểm \(C;D\) ta được đồ thị của hàm số \(y = - 2x - 6\).
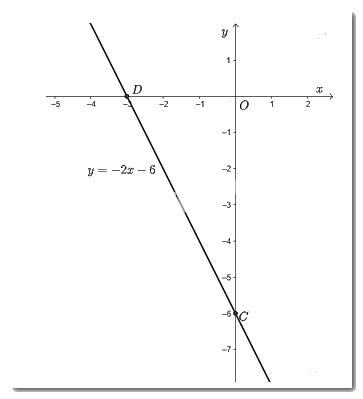
Video hướng dẫn giải
Cho hàm số \(y = f\left( x \right) = x\) và \(y = g\left( x \right) = x + 3\)
a) Thay dấu ? bằng số thích hợp.

b) Trên cùng một mặt phẳng tọa độ, vẽ đồ thị của hàm số \(y = f\left( x \right)\) và biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) có trong bảng trên.
c) Kiểm tra xem các điểm thuộc đồ thị hàm số của \(y = g\left( x \right)\) vẽ ở câu b có thẳng hàng không. Và dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\).
Phương pháp giải:
- Giá trị của hàm số \(y = f\left( x \right)\) tại điểm \(x = a\) là \(f\left( a \right)\).
- Vẽ đồ thị hàm số \(y = f\left( x \right)\) và biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) ta làm như sau:
Bước 1: Vẽ đồ thị hàm số \(y = f\left( x \right)\).
Bước 2: Biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\).
- Dùng thước thẳng kiểm tra các điểm thẳng hàng.
Lời giải chi tiết:
a)
- Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\);
- Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\);
- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);
- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);
- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\);
Ta có bảng sau:
\(x\) | –2 | –1 | 0 | 1 | 2 |
\(y = f\left( x \right) = x\) | –2 | –1 | 0 | 1 | 2 |
\(y = g\left( x \right) = x + 3\) | 1 | 2 | 3 | 4 | 5 |
b)
- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)
Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).
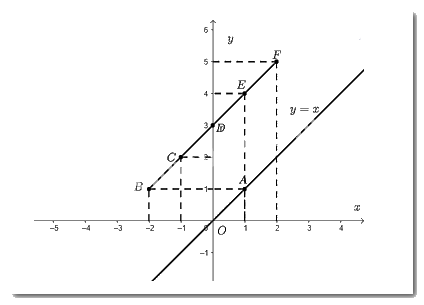
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.
Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):
Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).
Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).
Video hướng dẫn giải
a) Vẽ đồ thị của hàm số: \(y = 0,5x;y = - 3x;y = x\).
b) Các đồ thị sau đây là đồ thị của hàm số nào?
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\).
Để xác định một hàm số \(y = ax\) qua đồ thị ta lấy một điểm thuộc đồ thị và đi tìm ngược lại hệ số \(a\).
Lời giải chi tiết:
a)
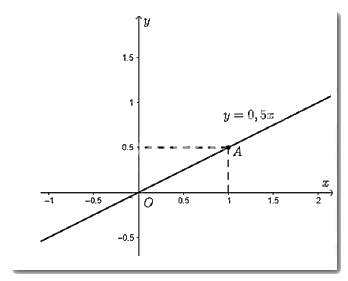
- Vẽ đồ thị hàm số \(y = 0,5x\)
Cho \(x = 1 \Rightarrow y = 0,5.1 = 0,5\). Ta vẽ điểm \(A\left( {1;0,5} \right)\)
Đồ thị hàm số \(y = 0,5x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;0,5} \right)\).
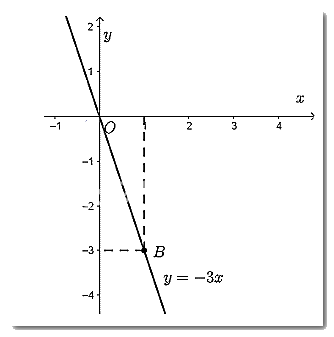
- Vẽ đồ thị hàm số \(y = - 3x\)
Cho \(x = 1 \Rightarrow y = - 3.1 = - 3\). Ta vẽ điểm \(B\left( {1; - 3} \right)\)
Đồ thị hàm số \(y = - 3x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(B\left( {1; - 3} \right)\).
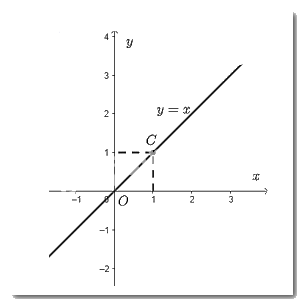
- Vẽ đồ thị hàm số \(y = x\)
Cho \(x = 1 \Rightarrow y = 1\). Ta vẽ điểm \(C\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(C\left( {1;1} \right)\).
b) Ta thấy cả ba đồ thị đều đi qua gốc tọa độ \(O\left( {0;0} \right)\) nên có dạng \(y = ax\).
- Ở đồ thị a, đồ thị hàm số đi qua điểm \(A\left( {1;2} \right)\) nên ta có: \(2 = a.1 \Rightarrow a = 2\).
Do đó, đồ thị a là đồ thị của hàm số \(y = 2x\).
- Ở đồ thị b, đồ thị hàm số đi qua điểm \(B\left( { - 2;2} \right)\) nên ta có: \(2 = a.\left( { - 2} \right) \Rightarrow a = 2:\left( { - 2} \right) = - 1\).
Do đó, đồ thị b là đồ thị của hàm số \(y = - x\).
- Ở đồ thị c, đồ thị hàm số đi qua điểm \(C\left( {2; - 1} \right)\) nên ta có: \( - 1 = a.2 \Rightarrow a = \left( { - 1} \right):2 = \dfrac{{ - 1}}{2}\).
Do đó, đồ thị b là đồ thị của hàm số \(y = \dfrac{{ - 1}}{2}x\).
Video hướng dẫn giải
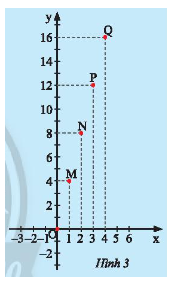
Hùng mua \(x\) mét dây điện và phải trả số tiền là \(y\) nghìn đồng. Giá trị tương ứng giữa \(x\)và \(y\) được cho bởi bảng sau:

Hùng vẽ các điểm \(M\left( {1;4} \right);N\left( {2;8} \right);P\left( {3;12} \right);Q\left( {4;16} \right)\) trên mặt phẳng tọa độ \(Oxy\) như Hình 3. Hãy dùng thước thẳng để kiểm tra các điểm \(O;M;N;P;Q\) có thẳng hàng không.
Phương pháp giải:
Dùng thước thẳng đặt vào các điểm để kiểm tra.
Lời giải chi tiết:
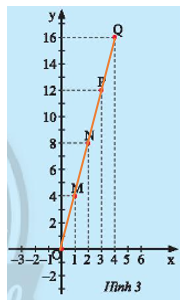
Dùng thước thẳng kiểm tra ta thấy các điểm \(O;M;N;P;Q\) thẳng hàng.
Video hướng dẫn giải
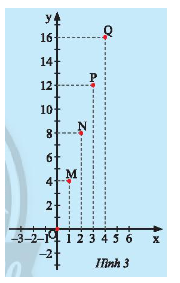
Hùng mua \(x\) mét dây điện và phải trả số tiền là \(y\) nghìn đồng. Giá trị tương ứng giữa \(x\)và \(y\) được cho bởi bảng sau:

Hùng vẽ các điểm \(M\left( {1;4} \right);N\left( {2;8} \right);P\left( {3;12} \right);Q\left( {4;16} \right)\) trên mặt phẳng tọa độ \(Oxy\) như Hình 3. Hãy dùng thước thẳng để kiểm tra các điểm \(O;M;N;P;Q\) có thẳng hàng không.
Phương pháp giải:
Dùng thước thẳng đặt vào các điểm để kiểm tra.
Lời giải chi tiết:
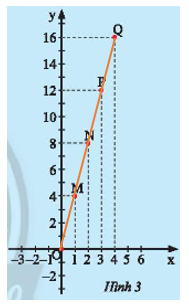
Dùng thước thẳng kiểm tra ta thấy các điểm \(O;M;N;P;Q\) thẳng hàng.
Video hướng dẫn giải
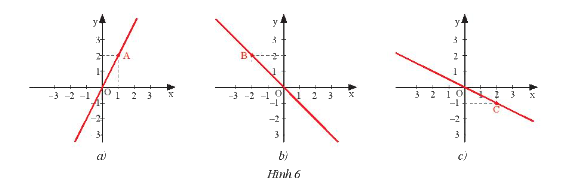
a) Vẽ đồ thị của hàm số: \(y = 0,5x;y = - 3x;y = x\).
b) Các đồ thị sau đây là đồ thị của hàm số nào?
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\).
Để xác định một hàm số \(y = ax\) qua đồ thị ta lấy một điểm thuộc đồ thị và đi tìm ngược lại hệ số \(a\).
Lời giải chi tiết:
a)
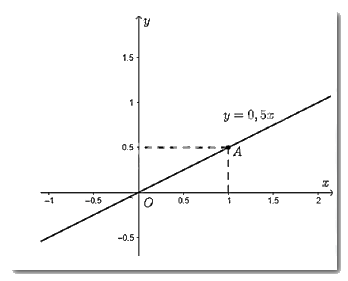
- Vẽ đồ thị hàm số \(y = 0,5x\)
Cho \(x = 1 \Rightarrow y = 0,5.1 = 0,5\). Ta vẽ điểm \(A\left( {1;0,5} \right)\)
Đồ thị hàm số \(y = 0,5x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;0,5} \right)\).
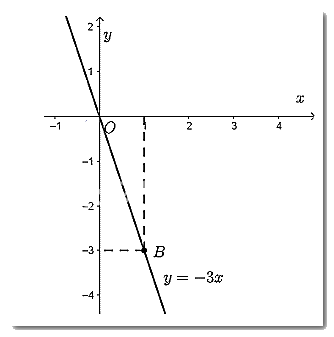
- Vẽ đồ thị hàm số \(y = - 3x\)
Cho \(x = 1 \Rightarrow y = - 3.1 = - 3\). Ta vẽ điểm \(B\left( {1; - 3} \right)\)
Đồ thị hàm số \(y = - 3x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(B\left( {1; - 3} \right)\).
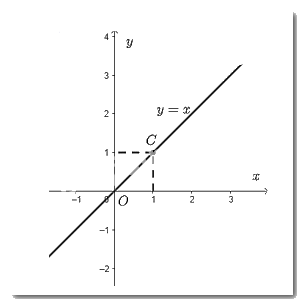
- Vẽ đồ thị hàm số \(y = x\)
Cho \(x = 1 \Rightarrow y = 1\). Ta vẽ điểm \(C\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(C\left( {1;1} \right)\).
b) Ta thấy cả ba đồ thị đều đi qua gốc tọa độ \(O\left( {0;0} \right)\) nên có dạng \(y = ax\).
- Ở đồ thị a, đồ thị hàm số đi qua điểm \(A\left( {1;2} \right)\) nên ta có: \(2 = a.1 \Rightarrow a = 2\).
Do đó, đồ thị a là đồ thị của hàm số \(y = 2x\).
- Ở đồ thị b, đồ thị hàm số đi qua điểm \(B\left( { - 2;2} \right)\) nên ta có: \(2 = a.\left( { - 2} \right) \Rightarrow a = 2:\left( { - 2} \right) = - 1\).
Do đó, đồ thị b là đồ thị của hàm số \(y = - x\).
- Ở đồ thị c, đồ thị hàm số đi qua điểm \(C\left( {2; - 1} \right)\) nên ta có: \( - 1 = a.2 \Rightarrow a = \left( { - 1} \right):2 = \dfrac{{ - 1}}{2}\).
Do đó, đồ thị b là đồ thị của hàm số \(y = \dfrac{{ - 1}}{2}x\).
Video hướng dẫn giải
Cho hàm số \(y = f\left( x \right) = x\) và \(y = g\left( x \right) = x + 3\)
a) Thay dấu ? bằng số thích hợp.

b) Trên cùng một mặt phẳng tọa độ, vẽ đồ thị của hàm số \(y = f\left( x \right)\) và biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) có trong bảng trên.
c) Kiểm tra xem các điểm thuộc đồ thị hàm số của \(y = g\left( x \right)\) vẽ ở câu b có thẳng hàng không. Và dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\).
Phương pháp giải:
- Giá trị của hàm số \(y = f\left( x \right)\) tại điểm \(x = a\) là \(f\left( a \right)\).
- Vẽ đồ thị hàm số \(y = f\left( x \right)\) và biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) ta làm như sau:
Bước 1: Vẽ đồ thị hàm số \(y = f\left( x \right)\).
Bước 2: Biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\).
- Dùng thước thẳng kiểm tra các điểm thẳng hàng.
Lời giải chi tiết:
a)
- Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\);
- Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\);
- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);
- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);
- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\);
Ta có bảng sau:
\(x\) | –2 | –1 | 0 | 1 | 2 |
\(y = f\left( x \right) = x\) | –2 | –1 | 0 | 1 | 2 |
\(y = g\left( x \right) = x + 3\) | 1 | 2 | 3 | 4 | 5 |
b)
- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)
Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).
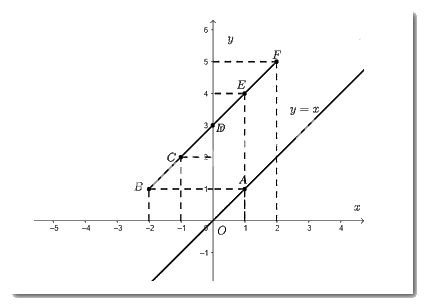
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.
Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):
Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).
Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).
Video hướng dẫn giải
Vẽ đồ thị của các hàm số sau:
a) \(y = 5x + 2\);
b) \(y = - 2x - 6\);
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\).
Lời giải chi tiết:
a) \(y = 5x + 2\);
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{5}\) ta được điểm \(B\left( {\dfrac{{ - 2}}{5};0} \right)\) trên \(Ox\).
Vẽ đường thẳng đi qua hai điểm \(A;B\) ta được đồ thị của hàm số \(y = 5x + 2\).
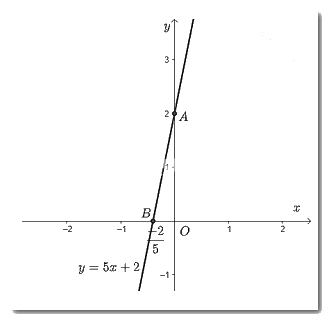
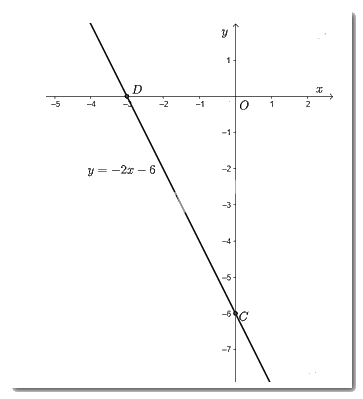
b) \(y = - 2x - 6\)
Cho \(x = 0 \Rightarrow y = - 6\) ta được điểm \(C\left( {0; - 6} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = - 3\) ta được điểm \(D\left( { - 3;0} \right)\) trên \(Ox\).
Vẽ đường thẳng đi qua hai điểm \(C;D\) ta được đồ thị của hàm số \(y = - 2x - 6\).
Video hướng dẫn giải
Một lò xo có chiều dài ban đầu khi chưa treo vật nặng là 10 cm. Cho biết treo thêm vào lò xo 1 vật nặng 1 kg thì chiều dài lò xo tăng thêm 3 cm.
a) Tính chiều dài \(y\) (cm) của lò xo theo khối lượng \(x\) (kg) của vật.
b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).
Phương pháp giải:
Độ dài của lò xo sau khi treo vật nặng bằng độ dài ban đầu của lò xo cộng với độ dài tăng thêm do bị ảnh hưởng của vật nặng.
Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\).
Lời giải chi tiết:
Vì cứ treo thêm 1 kg vật nặng thì lò xo dài thêm 3 cm nên treo thêm \(x\) kg vật nặng thì lò xo dài thêm \(3x\) cm.
Chiều dài của lò xo sau khi treo vật nặng là:
\(y = 3x + 10\).
b) Vẽ đồ thị hàm số \(y = 3x + 10\)
Cho \(x = 0 \Rightarrow y = 10\) ta được điểm \(M\left( {0;10} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 10}}{3}\) ta được điểm \(N\left( {\dfrac{{ - 10}}{3};0} \right)\) trên \(Ox\).
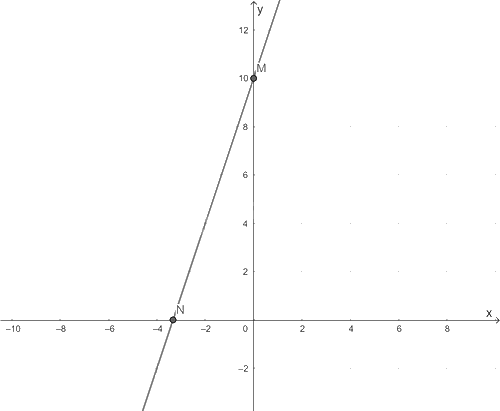
Đồ thị hàm số \(y = 3x + 10\) là đường thẳng đi qua hai điểm \(M;N\).
Mục 3 trong SGK Toán 8 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để hoàn thành tốt các bài tập này. Giaitoan.edu.vn sẽ cung cấp cho bạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ bản chất của vấn đề và cách tiếp cận hiệu quả.
Ở trang 18, các bài tập thường xoay quanh việc áp dụng các định nghĩa, tính chất đã học để chứng minh các đẳng thức, bất đẳng thức đơn giản. Ví dụ, bài tập 1 có thể yêu cầu chứng minh một biểu thức đại số tương đương với một biểu thức khác. Lời giải sẽ bao gồm các bước biến đổi đại số, sử dụng các quy tắc cộng, trừ, nhân, chia đa thức.
Trang 19 thường chứa các bài tập nâng cao hơn, đòi hỏi học sinh phải suy luận logic và kết hợp nhiều kiến thức khác nhau. Ví dụ, bài tập 4 có thể yêu cầu giải một phương trình bậc nhất một ẩn. Lời giải sẽ bao gồm các bước biến đổi phương trình, sử dụng các quy tắc chuyển vế, quy đồng mẫu số, và tìm nghiệm của phương trình.
Các bài tập trên trang 20 có thể liên quan đến việc giải bài toán thực tế, ứng dụng kiến thức Toán học vào các tình huống đời sống. Ví dụ, bài tập 7 có thể yêu cầu tính diện tích của một hình chữ nhật. Lời giải sẽ bao gồm các bước tính toán, sử dụng các công thức tính diện tích, chu vi, và các đơn vị đo lường.
Trang 21 thường là phần tổng hợp, ôn tập lại các kiến thức đã học trong mục 3. Các bài tập ở đây có thể là các bài tập trắc nghiệm, bài tập tự luận, hoặc bài tập kết hợp nhiều dạng khác nhau. Việc giải các bài tập này sẽ giúp học sinh củng cố kiến thức và chuẩn bị cho các bài kiểm tra, thi cử.
Giaitoan.edu.vn cam kết cung cấp cho bạn những lời giải bài tập Toán 8 chính xác, dễ hiểu, và đầy đủ. Chúng tôi luôn cập nhật những kiến thức mới nhất và phương pháp giải bài tập hiệu quả nhất. Hãy truy cập giaitoan.edu.vn để học tập và khám phá thế giới Toán học!
| Bài tập | Trang | Lời giải |
|---|---|---|
| Bài tập 1 | 18 | Xem lời giải |
| Bài tập 2 | 18 | Xem lời giải |
| Bài tập 3 | 19 | Xem lời giải |