Bài 10 trang 85 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 85 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
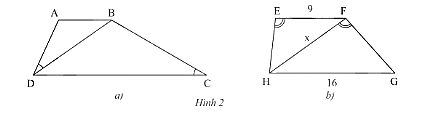
a) Cho hình thang
Đề bài
a) Cho hình thang \(ABCD\left( {AB//CD} \right)\), biết \(\widehat {ADB} = \widehat {DCB}\) (Hình 2a).
Chứng minh rằng \(B{D^2} = AB.CD\).
b) Cho hình thang \(EFGH\left( {FF//GH} \right),\widehat {HEF} = \widehat {HFG},EF = 9m,GH = 16m\) (Hình 2b).
Tính độ dài \(x\) của \(HF\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = k\)
Lời giải chi tiết
a) Vì \(ABCD\) là hình thang có \(AB//CD\) nên \(\widehat {ABD} = \widehat {BDC}\) (hai góc so le trong)
Xét tam giác \(ABD\) và tam giác \(BDC\) có:
\(\widehat {ADB} = \widehat {DCB}\) (giả thuyết)
\(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên)
Suy ra, \(\Delta ABD\backsim\Delta BDC\) (g.g)
Suy ra, \(\frac{{AB}}{{BD}} = \frac{{BD}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(B{D^2} = AB.CD\).
b) Vì \(EFGH\) là hình thang có \(FF//GH\) nên \(\widehat {EFH} = \widehat {FHG}\) (hai góc so le trong)
Xét tam giác \(EFH\) và tam giác \(FHG\) có:
\(\widehat {HEF} = \widehat {HFG}\) (giả thuyết)
\(\widehat {EFH} = \widehat {FHG}\) (chứng minh trên)
Suy ra, \(\Delta EFH\backsim\Delta FHG\) (g.g)
Suy ra, \(\frac{{EF}}{{FH}} = \frac{{FH}}{{HG}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(F{H^2} = EF.HG = 9.16 = 144 \) nên \(FH = \sqrt {144} = 12\).
Vậy \(FH = 12cm\).
Bài 10 trang 85 SGK Toán 8 tập 2 – Chân trời sáng tạo thường xoay quanh việc áp dụng các quy tắc về phép nhân đa thức, phép chia đa thức và các hằng đẳng thức đáng nhớ. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài tập. Tuy nhiên, dưới đây là một ví dụ về cách tiếp cận giải một bài tập tương tự:
Giả sử bài tập yêu cầu phân tích đa thức thành nhân tử: x^2 - 4x + 4
Để học tốt Toán 8 tập 2 và giải quyết các bài tập một cách hiệu quả, bạn nên:
Bài 10 trang 85 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán trên đa thức. Bằng cách nắm vững lý thuyết, luyện tập thường xuyên và sử dụng các nguồn tài liệu hỗ trợ, các em học sinh có thể tự tin giải quyết bài tập và đạt kết quả tốt trong môn Toán.