Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 – Chân trời sáng tạo. Mục 1 trang 19, 20 là phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức cơ bản và kỹ năng giải bài tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải đáp này để hỗ trợ bạn tối đa.
a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích (S) của các phần tô màu trong Hình 1 như sau:
Video hướng dẫn giải
Tính:
a) \({\left( {3x + 1} \right)^2}\)
b) \({\left( {4x + 5y} \right)^2}\)
c) \({\left( {5x - \dfrac{1}{2}} \right)^2}\)
d) \({\left( { - x + 2{y^2}} \right)^2}\)
Phương pháp giải:
Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu
\(\begin{array}{l}{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\\{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\end{array}\)
Lời giải chi tiết:
a) \({\left( {3x + 1} \right)^2} = {\left( {3x} \right)^2} + 2.3x.1 + {1^2} = 9{x^2} + 6x + 1\)
b) \({\left( {4x + 5y} \right)^2} = {\left( {4x} \right)^2} + 2.4x.5y + {\left( {5y} \right)^2} = 16{x^2} + 40xy + 25{y^2}\)
c) \({\left( {5x - \dfrac{1}{2}} \right)^2} = {\left( {5x} \right)^2} - 2.5x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = 25{x^2} - 5x + \dfrac{1}{4}\)
d) \({\left( { - x + 2{y^2}} \right)^2} = {\left( { - x} \right)^2} + 2.\left( { - x} \right).\left( {2{y^2}} \right) + {\left( {2{y^2}} \right)^2} = {x^2} - 4x{y^2} + 4{y^4}\)
Video hướng dẫn giải
Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:
a) \({a^2} + 10ab + 25{b^2}\)
b) \(1 + 9{a^2} - 6a\)
Phương pháp giải:
Đưa biểu thức về dạng vế phải của hai hằng đẳng thức: Bình phương của một tổng, một hiệu
\(\begin{array}{l}{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\\{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\end{array}\)
Lời giải chi tiết:
a) \({a^2} + 10ab + 25{b^2} = {a^2} + 2.a.5b + {\left( {5b} \right)^2} = {\left( {a + 5b} \right)^2}\)
b) \(1 + 9{a^2} - 6a = 1 - 6a + 9{a^2} = 1 - 2.1.3a + {\left( {3a} \right)^2} = {\left( {1 - 3a} \right)^2}\)
Video hướng dẫn giải
Tính nhanh:
a) \({52^2}\)
b) \({98^2}\)
Phương pháp giải:
Tách số đã cho thành tổng hoặc hiệu của một số tròn chục với một số tự nhiên.
Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu
Lời giải chi tiết:
a) \({52^2} = {\left( {50 + 2} \right)^2} = {50^2} + 2.50.2 + {2^2} = 2500 + 200 + 4 = 2704\)
b) \({98^2} = {\left( {100 - 2} \right)^2} = {100^2} - 2.100.2 + {2^2} = 10000 - 400 + 4 = 9604\)
Video hướng dẫn giải
a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích \(S\) của các phần tô màu trong Hình 1 như sau:
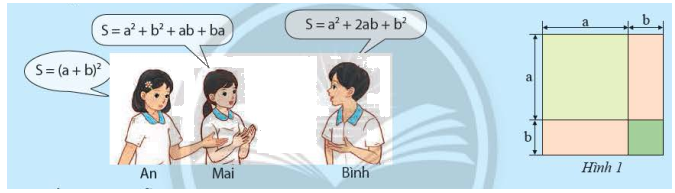
Kết quả của mỗi bạn có đúng không? Giải thích.
b) Thực hiện phép nhân và rút gọn đa thức của bạn An.
c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức \({\left( {a - b} \right)^2}\) thành biểu thức nào?
Phương pháp giải:
Áp dụng quy tắc nhân đa thức.
Lời giải chi tiết:
a) Chiều dài và chiều rộng của hình 1 lần lượt là \(a + b\), \(a + b\)
Tổng diện tích \(S\) của hình 1 là:
\(S = \left( {a + b} \right)\left( {a + b} \right) = a.a + ab + ba + b.b = {a^2} + ab + ba + {b^2} = {a^2} + 2ab + {b^2}\) hay \(S = {\left( {a + b} \right)^2} = {a^2} + {b^2} + ab + ba = {a^2} + 2ab + {b^2}\)
Vậy cả ba bạn An, Mai và Bình đều nói đúng kết quả.
b) \(S = {\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {a + b} \right) = a.a + ab + ba + b.b = {a^2} + 2ab + {b^2}\)
c) Ta có: \({\left( {a - b} \right)^2} = \left( {a - b} \right)\left( {a - b} \right) = a.a - ab - ba + b.b = {a^2} - 2ab + {b^2}\)
Video hướng dẫn giải
a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích \(S\) của các phần tô màu trong Hình 1 như sau:
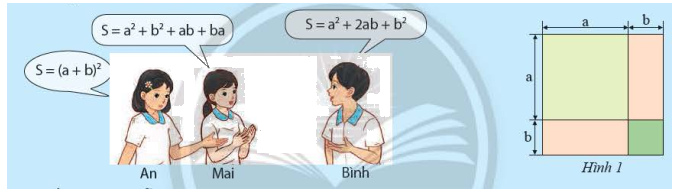
Kết quả của mỗi bạn có đúng không? Giải thích.
b) Thực hiện phép nhân và rút gọn đa thức của bạn An.
c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức \({\left( {a - b} \right)^2}\) thành biểu thức nào?
Phương pháp giải:
Áp dụng quy tắc nhân đa thức.
Lời giải chi tiết:
a) Chiều dài và chiều rộng của hình 1 lần lượt là \(a + b\), \(a + b\)
Tổng diện tích \(S\) của hình 1 là:
\(S = \left( {a + b} \right)\left( {a + b} \right) = a.a + ab + ba + b.b = {a^2} + ab + ba + {b^2} = {a^2} + 2ab + {b^2}\) hay \(S = {\left( {a + b} \right)^2} = {a^2} + {b^2} + ab + ba = {a^2} + 2ab + {b^2}\)
Vậy cả ba bạn An, Mai và Bình đều nói đúng kết quả.
b) \(S = {\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {a + b} \right) = a.a + ab + ba + b.b = {a^2} + 2ab + {b^2}\)
c) Ta có: \({\left( {a - b} \right)^2} = \left( {a - b} \right)\left( {a - b} \right) = a.a - ab - ba + b.b = {a^2} - 2ab + {b^2}\)
Video hướng dẫn giải
Tính:
a) \({\left( {3x + 1} \right)^2}\)
b) \({\left( {4x + 5y} \right)^2}\)
c) \({\left( {5x - \dfrac{1}{2}} \right)^2}\)
d) \({\left( { - x + 2{y^2}} \right)^2}\)
Phương pháp giải:
Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu
\(\begin{array}{l}{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\\{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\end{array}\)
Lời giải chi tiết:
a) \({\left( {3x + 1} \right)^2} = {\left( {3x} \right)^2} + 2.3x.1 + {1^2} = 9{x^2} + 6x + 1\)
b) \({\left( {4x + 5y} \right)^2} = {\left( {4x} \right)^2} + 2.4x.5y + {\left( {5y} \right)^2} = 16{x^2} + 40xy + 25{y^2}\)
c) \({\left( {5x - \dfrac{1}{2}} \right)^2} = {\left( {5x} \right)^2} - 2.5x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = 25{x^2} - 5x + \dfrac{1}{4}\)
d) \({\left( { - x + 2{y^2}} \right)^2} = {\left( { - x} \right)^2} + 2.\left( { - x} \right).\left( {2{y^2}} \right) + {\left( {2{y^2}} \right)^2} = {x^2} - 4x{y^2} + 4{y^4}\)
Video hướng dẫn giải
Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:
a) \({a^2} + 10ab + 25{b^2}\)
b) \(1 + 9{a^2} - 6a\)
Phương pháp giải:
Đưa biểu thức về dạng vế phải của hai hằng đẳng thức: Bình phương của một tổng, một hiệu
\(\begin{array}{l}{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\\{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\end{array}\)
Lời giải chi tiết:
a) \({a^2} + 10ab + 25{b^2} = {a^2} + 2.a.5b + {\left( {5b} \right)^2} = {\left( {a + 5b} \right)^2}\)
b) \(1 + 9{a^2} - 6a = 1 - 6a + 9{a^2} = 1 - 2.1.3a + {\left( {3a} \right)^2} = {\left( {1 - 3a} \right)^2}\)
Video hướng dẫn giải
Tính nhanh:
a) \({52^2}\)
b) \({98^2}\)
Phương pháp giải:
Tách số đã cho thành tổng hoặc hiệu của một số tròn chục với một số tự nhiên.
Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu
Lời giải chi tiết:
a) \({52^2} = {\left( {50 + 2} \right)^2} = {50^2} + 2.50.2 + {2^2} = 2500 + 200 + 4 = 2704\)
b) \({98^2} = {\left( {100 - 2} \right)^2} = {100^2} - 2.100.2 + {2^2} = 10000 - 400 + 4 = 9604\)
Video hướng dẫn giải
a) Một mảnh vườn hình vuông có cạnh \(10\)m được mở rộng cả hai cạnh thêm \(x\) (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng.
b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh \(5\)m thì được một mảnh vườn hình vuông có cạnh là \(x\) (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng.
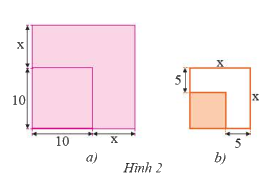
Phương pháp giải:
Áp dụng công thức tính diện tích hình vuông
Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu.
Lời giải chi tiết:
a) Độ dài cạnh mảnh vườn hình vuông sau khi mở rộng là: \(x + 10\) (m)
Diện tích mảnh vườn sau khi mở rộng là:
\(\left( {x + 10} \right)\left( {x + 10} \right) = {\left( {x + 10} \right)^2} = {x^2} + 2.x.10 + {10^2} = {x^2} + 20x + 100\) (\({m^2}\))
b) Độ dài cạnh mảnh vườn hình vuông trước khi mở rộng là: \(x - 5\) (m)
Diện tích mảnh vườn hình vuông trước khi mở rộng là: \(\left( {x - 5} \right)\left( {x - 5} \right) = {\left( {x - 5} \right)^2} = {x^2} - 2.x.5 + {5^2} = {x^2} - 10x + 25\) (\({m^2}\))
Video hướng dẫn giải
a) Một mảnh vườn hình vuông có cạnh \(10\)m được mở rộng cả hai cạnh thêm \(x\) (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng.
b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh \(5\)m thì được một mảnh vườn hình vuông có cạnh là \(x\) (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng.
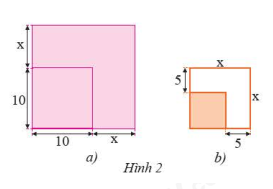
Phương pháp giải:
Áp dụng công thức tính diện tích hình vuông
Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu.
Lời giải chi tiết:
a) Độ dài cạnh mảnh vườn hình vuông sau khi mở rộng là: \(x + 10\) (m)
Diện tích mảnh vườn sau khi mở rộng là:
\(\left( {x + 10} \right)\left( {x + 10} \right) = {\left( {x + 10} \right)^2} = {x^2} + 2.x.10 + {10^2} = {x^2} + 20x + 100\) (\({m^2}\))
b) Độ dài cạnh mảnh vườn hình vuông trước khi mở rộng là: \(x - 5\) (m)
Diện tích mảnh vườn hình vuông trước khi mở rộng là: \(\left( {x - 5} \right)\left( {x - 5} \right) = {\left( {x - 5} \right)^2} = {x^2} - 2.x.5 + {5^2} = {x^2} - 10x + 25\) (\({m^2}\))
Mục 1 của chương trình Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán cơ bản, các biểu thức đại số đơn giản và các bài toán liên quan đến số thực. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài 1 yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, cần nhớ lại các quy tắc sau:
Ví dụ: Tính (-2/3) + (1/2)
Giải:
Để cộng hai phân số này, ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 3 và 2 là 6. Ta có:
(-2/3) = (-4/6) và (1/2) = (3/6)
Vậy, (-2/3) + (1/2) = (-4/6) + (3/6) = (-1/6)
Bài 2 tập trung vào việc thu gọn các biểu thức đại số đơn giản. Để thu gọn biểu thức, ta cần thực hiện các phép toán cộng, trừ các đơn thức đồng dạng.
Ví dụ: Thu gọn biểu thức 3x + 2y - x + 5y
Giải:
Ta có các đơn thức đồng dạng là 3x và -x, 2y và 5y. Ta thu gọn như sau:
3x + 2y - x + 5y = (3x - x) + (2y + 5y) = 2x + 7y
Bài 3 thường là các bài toán ứng dụng thực tế liên quan đến số thực. Để giải bài tập này, cần đọc kỹ đề bài, xác định các đại lượng liên quan và lập phương trình hoặc biểu thức phù hợp.
Ví dụ: Một người mua 3 kg táo với giá 20.000 đồng/kg và 2 kg cam với giá 15.000 đồng/kg. Hỏi người đó phải trả bao nhiêu tiền?
Giải:
Số tiền mua táo là: 3 kg * 20.000 đồng/kg = 60.000 đồng
Số tiền mua cam là: 2 kg * 15.000 đồng/kg = 30.000 đồng
Tổng số tiền người đó phải trả là: 60.000 đồng + 30.000 đồng = 90.000 đồng
Hy vọng với bộ giải đáp chi tiết này, bạn sẽ học tốt Mục 1 trang 19, 20 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc bạn thành công!