Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 6 và 7 sách giáo khoa Toán 8 – Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập về nhà. Hãy cùng bắt đầu nhé!
a) Nhiệt độ cơ thể
Video hướng dẫn giải
Khi đo nhiệt độ, ta có công thức đổi từ đơn vị độ C (Celsius) sang đơn vị độ F (Fahrenheit) như sau: F = 1,8C + 3,2. Theo em, F có phải làm một hàm số theo biến số C hay không? Giải thích.
Phương pháp giải:
Nếu đại lượng y phụ thuộc vào một đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y được gọi làm số của biến số x.
Lời giải chi tiết:
F là một hàm số theo biến C vì với mỗi giá trị của C chỉ cho ta duy nhất một giá trị của F.
Video hướng dẫn giải
a) Nhiệt độ cơ thể d \(\left( {^\circ C} \right)\) của bệnh nhân theo thời gian h (giờ) trong ngày được ghi trong bảng sau:

Ứng với mỗi giờ em đọc được bao nhiêu số chỉ nhiệt độ?
b) Thời gian \(t\) (giờ) để một vật chuyển động đều đi hết quãng đường 180 km tỉ lệ nghịch với vận tốc \(v\) (km/h) của nó theo công thức \(t = \dfrac{{180}}{v}\).
Tính và lập bảng các giá trị tương ứng của \(t\) và \(v\) lần lượt bằng 10; 20; 30; 60; 180.
Ứng với mỗi giá trị của đại lượng \(v\) em tính được bao nhiêu giá trị của đại lượng \(t\)?
Phương pháp giải:
a) Quan sát và đọc bảng số liệu.
b) Tính toán các giá trị bằng cách thay vào công thức sau đó kẻ bảng với các gá trị tìm được.
Lời giải chi tiết:
a) Ứng với mỗi giờ chỉ đọc được một số chỉ nhiệt độ.
Ứng với 7h thì nhiệt độ là \(36^\circ C\)
Ứng với 8h thì nhiệt độ là \(37^\circ C\)
Ứng với 9h thì nhiệt độ là \(36^\circ C\)
Ứng với 10h thì nhiệt độ là \(37^\circ C\)
Ứng với 11h thì nhiệt độ là \(38^\circ C\)
Ứng với 12h thì nhiệt độ là \(37^\circ C\)
Ứng với 13h thì nhiệt độ là \(38^\circ C\)
Ứng với 14h thì nhiệt độ là \(39^\circ C\)
Ứng với 15h thì nhiệt độ là \(39^\circ C\)
b) Với \(v = 10 \Rightarrow t = \dfrac{{180}}{{10}} = 18\)
Với \(v = 20 \Rightarrow t = \dfrac{{180}}{{20}} = 9\)
Với \(v = 30 \Rightarrow t = \dfrac{{180}}{{30}} = 6\)
Với \(v = 60 \Rightarrow t = \dfrac{{180}}{{60}} = 3\)
Với \(v = 180 \Rightarrow t = \dfrac{{180}}{{180}} = 1\)
Lập bảng:
\(v\) | 10 | 20 | 30 | 60 | 180 |
\(t\) | 18 | 9 | 6 | 3 | 1 |
Video hướng dẫn giải
Mô tả các đại lượng là hàm số và biến số trong các mô hình sau:
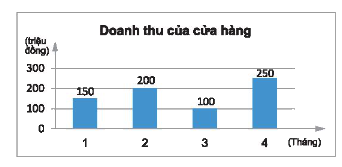
a) Biểu đồ cột chỉ doanh thu \(y\) (triệu đồng) của một cửa hàng trong các tháng \(x\).
b) Quãng đường \(s\) (km) đi được trong khoảng thời gian \(t\) (giờ) của một chiếc xe chạy với tốc độ không đổi bằng 40 km/h.
c) Số tiền \(y\) (đồng) người mua phải trả cho \(x\) quyển vở có giá trị 10 000 đồng/ quyển.
Phương pháp giải:
Nếu đại lượng \(y\) phụ thuộc vào một đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x\) ta luôn xác định được duy nhất một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của biến số \(x\).
Lời giải chi tiết:
a) Đại lượng là hàm số là doanh thu (triệu đồng) của một cửa hàng và biến số là tháng x.
b) Đại lượng là hàm số là quãng đường đi được và biến số là thời gian .
c) Đại lượng là hàm số là số tiền người mua phải trả và biến số là số quyển vở.
Video hướng dẫn giải
Khi đo nhiệt độ, ta có công thức đổi từ đơn vị độ C (Celsius) sang đơn vị độ F (Fahrenheit) như sau: F = 1,8C + 3,2. Theo em, F có phải làm một hàm số theo biến số C hay không? Giải thích.
Phương pháp giải:
Nếu đại lượng y phụ thuộc vào một đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được duy nhất một giá trị tương ứng của y được gọi làm số của biến số x.
Lời giải chi tiết:
F là một hàm số theo biến C vì với mỗi giá trị của C chỉ cho ta duy nhất một giá trị của F.
Video hướng dẫn giải
Mô tả các đại lượng là hàm số và biến số trong các mô hình sau:
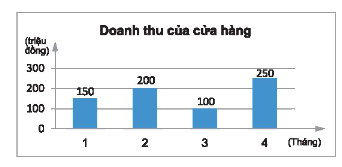
a) Biểu đồ cột chỉ doanh thu \(y\) (triệu đồng) của một cửa hàng trong các tháng \(x\).
b) Quãng đường \(s\) (km) đi được trong khoảng thời gian \(t\) (giờ) của một chiếc xe chạy với tốc độ không đổi bằng 40 km/h.
c) Số tiền \(y\) (đồng) người mua phải trả cho \(x\) quyển vở có giá trị 10 000 đồng/ quyển.
Phương pháp giải:
Nếu đại lượng \(y\) phụ thuộc vào một đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x\) ta luôn xác định được duy nhất một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của biến số \(x\).
Lời giải chi tiết:
a) Đại lượng là hàm số là doanh thu (triệu đồng) của một cửa hàng và biến số là tháng x.
b) Đại lượng là hàm số là quãng đường đi được và biến số là thời gian .
c) Đại lượng là hàm số là số tiền người mua phải trả và biến số là số quyển vở.
Video hướng dẫn giải
a) Nhiệt độ cơ thể d \(\left( {^\circ C} \right)\) của bệnh nhân theo thời gian h (giờ) trong ngày được ghi trong bảng sau:

Ứng với mỗi giờ em đọc được bao nhiêu số chỉ nhiệt độ?
b) Thời gian \(t\) (giờ) để một vật chuyển động đều đi hết quãng đường 180 km tỉ lệ nghịch với vận tốc \(v\) (km/h) của nó theo công thức \(t = \dfrac{{180}}{v}\).
Tính và lập bảng các giá trị tương ứng của \(t\) và \(v\) lần lượt bằng 10; 20; 30; 60; 180.
Ứng với mỗi giá trị của đại lượng \(v\) em tính được bao nhiêu giá trị của đại lượng \(t\)?
Phương pháp giải:
a) Quan sát và đọc bảng số liệu.
b) Tính toán các giá trị bằng cách thay vào công thức sau đó kẻ bảng với các gá trị tìm được.
Lời giải chi tiết:
a) Ứng với mỗi giờ chỉ đọc được một số chỉ nhiệt độ.
Ứng với 7h thì nhiệt độ là \(36^\circ C\)
Ứng với 8h thì nhiệt độ là \(37^\circ C\)
Ứng với 9h thì nhiệt độ là \(36^\circ C\)
Ứng với 10h thì nhiệt độ là \(37^\circ C\)
Ứng với 11h thì nhiệt độ là \(38^\circ C\)
Ứng với 12h thì nhiệt độ là \(37^\circ C\)
Ứng với 13h thì nhiệt độ là \(38^\circ C\)
Ứng với 14h thì nhiệt độ là \(39^\circ C\)
Ứng với 15h thì nhiệt độ là \(39^\circ C\)
b) Với \(v = 10 \Rightarrow t = \dfrac{{180}}{{10}} = 18\)
Với \(v = 20 \Rightarrow t = \dfrac{{180}}{{20}} = 9\)
Với \(v = 30 \Rightarrow t = \dfrac{{180}}{{30}} = 6\)
Với \(v = 60 \Rightarrow t = \dfrac{{180}}{{60}} = 3\)
Với \(v = 180 \Rightarrow t = \dfrac{{180}}{{180}} = 1\)
Lập bảng:
\(v\) | 10 | 20 | 30 | 60 | 180 |
\(t\) | 18 | 9 | 6 | 3 | 1 |
Mục 1 của chương trình Toán 8 – Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán cơ bản, các biểu thức đại số và các bài toán liên quan đến số thực. Việc nắm vững kiến thức nền tảng này là vô cùng quan trọng để các em có thể tiếp thu các kiến thức mới trong các chương tiếp theo.
Bài tập này yêu cầu các em thu gọn các đa thức đã cho bằng cách cộng các đơn thức đồng dạng. Để thu gọn một đa thức, các em cần thực hiện các bước sau:
Ví dụ: Thu gọn đa thức 3x2 + 2x - x2 + 5x. Ta có:
Bài tập này yêu cầu các em tính giá trị của một biểu thức đại số khi biết giá trị của các biến. Để tính giá trị của một biểu thức đại số, các em cần thực hiện các bước sau:
Ví dụ: Tính giá trị của biểu thức 2x + 3y khi x = 1 và y = 2. Ta có:
Bài tập này thường yêu cầu các em vận dụng kiến thức đã học để giải quyết các bài toán thực tế. Để giải quyết các bài toán thực tế, các em cần:
Ví dụ: Một khu vườn hình chữ nhật có chiều dài 10m và chiều rộng 5m. Tính diện tích của khu vườn.
Hy vọng rằng với lời giải chi tiết và dễ hiểu này, các em sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 6, 7 SGK Toán 8 – Chân trời sáng tạo. Chúc các em học tập tốt!