Bài 9 trang 89 SGK Toán 8 tập 1 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9 trang 89 SGK Toán 8 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác
Đề bài
Cho tam giác \(ABC\) cân tại \(A\). Gọi \(H\), \(D\) lần lượt là trung điểm của các cạnh \(BC\) và \(AB\)
a) Chứng minh rằng tứ giác \(ADHC\) là hình thang
b) Gọi \(E\) là điểm đối xứng với \(H\) qua \(D\). Chứng minh rằng tứ giác \(AHBE\) là hình chữ nhật
c) Tia \(CD\) cắt \(AH\) tại \(M\) và cắt \(BE\) tại \(N\). Chứng minh rằng tứ giác \(AMBN\) là hình bình hành.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Áp dụng dấu hiệu nhận biết của hình thang
b) Áp dụng dấu hiệu nhận biết của hình chữ nhật
c) Áp dụng dấu hiệu nhận biết của hình bình hành
Lời giải chi tiết
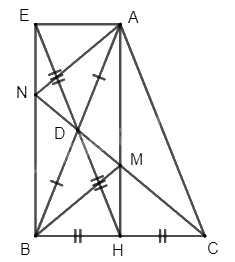
a) Vì \(\Delta ABC\) cân tại \(A\) nên \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)
Vì \(\Delta ABC\) cân tại \(A\), có \(AH\) là trung tuyến (gt)
Suy ra \(AH\) là đường cao
Suy ra \(AH \bot BC\)
Suy ra \(\widehat {{\rm{AHB}}} = \widehat {{\rm{AHC}}} = 90^\circ \)
Xét \(\Delta AHB\) vuông tại \(H\) ta có: \(HD\) là trung tuyến
Suy ra \(HD = \frac{1}{2}AB\)
Mà \(DA = DB = \frac{1}{2}AB\) (do \(D\) là trung điểm \(AB\))
Suy ra \(DA = DB = HD\)
Suy ra \(\Delta DHB\) cân tại \(D\)
Suy ra \(\widehat {{\rm{ABC}}} = \widehat {{\rm{DHB}}}\)
Mà \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)
Suy ra \(\widehat {{\rm{DHB}}} = \widehat {{\rm{ACB}}}\)
Mà hai góc ở vị trí đồng vị
Suy ra \(DH\) // \(AC\)
Suy ra \(ADHC\) là hình thang
b) Vì \(E\) đối xứng với \(H\) qua \(D\) (gt)
Suy ra \(D\) là trung điểm của \(HE\)
Xét tứ giác \(AHBE\) ta có:
Hai đường chéo \(HE\) và \(AB\) cắt nhau tại trung điểm \(D\)
Suy ra \(AHBE\) là hình bình hành
Mà \(\widehat {{\rm{AHB}}} = 90^\circ \) (cmt)
Suy ra \(AHBE\) là hình chữ nhật
c) Vì \(AHBE\) là hình chữ nhật (cmt)
Suy ra \(AH\) // \(BE\) và \(AH = BE\)
Xét \(\Delta DEN\) và \(\Delta DHM\) ta có:
\(\widehat {{\rm{NED}}} = \widehat {{\rm{DHM}}}\) (do \(BE\) // \(AH\))
\(DE = DH\) (do \(D\) là trung điểm của \(HE\))
\(\widehat {{\rm{EDN}}} = \widehat {{\rm{MDH}}}\) (đối đỉnh)
Suy ra \(\Delta DEN = \Delta DHM\) (g-c-g)
Suy ra \(EN = MH\) (hai cạnh tương ứng)
Mà \(BE = AH\) (cmt)
Suy ra \(BE - EN = AH - MH\)
Suy ra \(NB = AM\)
Mà \(NB\) // \(AM\) (do \(EB\) // \(AH\))
Suy ra \(AMBN\) là hình bình hành
Bài 9 trang 89 SGK Toán 8 tập 1 – Chân trời sáng tạo là một bài tập thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về phân tích đa thức thành nhân tử và các phép biến đổi đại số cơ bản. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức nền tảng và thực hành thường xuyên.
Bài 9 yêu cầu học sinh thực hiện các phép tính và biến đổi đại số để tìm ra kết quả cuối cùng. Thông thường, bài tập sẽ bao gồm các biểu thức chứa biến, các phép cộng, trừ, nhân, chia và các dấu ngoặc. Việc hiểu rõ thứ tự thực hiện các phép tính là rất quan trọng để tránh sai sót.
Để giải bài 9 trang 89 SGK Toán 8 tập 1, học sinh có thể áp dụng các phương pháp sau:
Dưới đây là lời giải chi tiết cho bài 9 trang 89 SGK Toán 8 tập 1 – Chân trời sáng tạo:
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, giải thích rõ ràng và kết quả cuối cùng. Ví dụ:)
Ví dụ: Giả sử bài tập yêu cầu tính giá trị của biểu thức (x + 2)(x - 2). Ta có thể áp dụng hằng đẳng thức (a + b)(a - b) = a2 - b2 để giải quyết bài toán này.
(x + 2)(x - 2) = x2 - 22 = x2 - 4
Khi giải bài 9 trang 89 SGK Toán 8 tập 1, học sinh cần lưu ý những điều sau:
Để củng cố kiến thức và kỹ năng giải toán, học sinh có thể tham khảo các bài tập tương tự sau:
Bài 9 trang 89 SGK Toán 8 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bằng cách nắm vững kiến thức nền tảng, áp dụng các phương pháp giải phù hợp và thực hành thường xuyên, học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn giải bài 9 trang 89 SGK Toán 8 tập 1 – Chân trời sáng tạo sẽ giúp các em học sinh học tập tốt hơn và đạt kết quả cao trong môn Toán.