Chào mừng bạn đến với bài học lý thuyết Nhân, chia phân thức thuộc chương trình Toán 8 - Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về các phép toán này với phân thức.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất và các quy tắc thực hiện phép nhân, chia phân thức một cách chi tiết và dễ hiểu. Đồng thời, bài học cũng sẽ cung cấp các ví dụ minh họa và bài tập vận dụng để giúp bạn củng cố kiến thức.
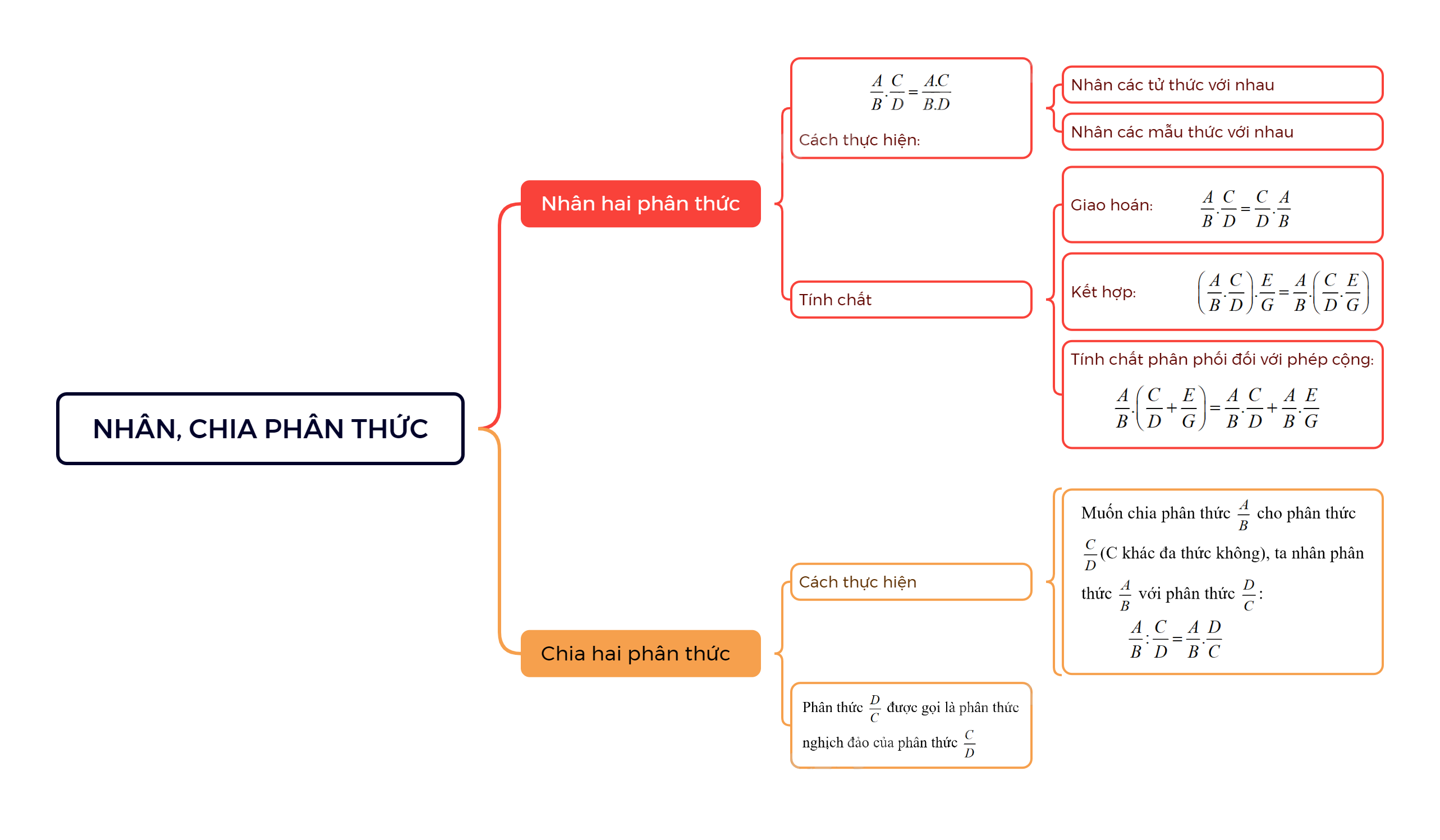
Nhân hai phân thức
1. Nhân hai phân thức
Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau.
\(\frac{A}{B}.\frac{C}{D} = \frac{{A.C}}{{B.D}}\)
2. Tính chất
- Giao hoán: \(\frac{A}{B}.\frac{C}{D} = \frac{C}{D}.\frac{A}{B}\)
- Kết hợp: \(\left( {\frac{A}{B}.\frac{C}{D}} \right).\frac{E}{G} = \frac{A}{B}.\left( {\frac{C}{D}.\frac{E}{G}} \right)\)
- Tính chất phân phối đối với phép cộng: \(\frac{A}{B}.\left( {\frac{C}{D} + \frac{E}{G}} \right) = \frac{A}{B}.\frac{C}{D} + \frac{A}{B}.\frac{E}{G}\)
Ví dụ:
\(\frac{{2xz}}{{3y}}.\frac{{ - 6{y^3}}}{{8{x^2}z}} = \frac{{2xz.( - 6{y^3})}}{{3y.8{x^2}z}} = \frac{{ - {y^2}}}{{2x}}\);
\(\frac{{{x^2} - 1}}{{{x^2} + 4x}}.\frac{{2x}}{{x - 1}} = \frac{{(x - 1)(x + 1).2x}}{{x(x + 4)(x - 1)}} = \frac{{2(x + 1)}}{{x + 4}}\)
3. Chia hai phân thức
Muốn chia phân thức \(\frac{A}{B}\) cho phân thức \(\frac{C}{D}\)(C khác đa thức không), ta nhân phân thức \(\frac{A}{B}\) với phân thức \(\frac{D}{C}\): \(\frac{A}{B}:\frac{C}{D} = \frac{A}{B}.\frac{D}{C}\)
Nhận xét: Phân thức \(\frac{D}{C}\) được gọi là phân thức nghịch đảo của phân thức \(\frac{C}{D}\)
Ví dụ:
\(\begin{array}{l}\frac{{{x^2} - 9}}{{x - 2}}:\frac{{x - 3}}{x} = \frac{{(x - 3)(x + 3)}}{{x - 2}}.\frac{x}{{x - 3}} = \frac{{(x - 3)(x + 3).x}}{{(x - 2)(x - 3)}} = \frac{{x(x + 3)}}{{x - 2}}\\\frac{x}{{{z^2}}}.\frac{{xz}}{{{y^3}}}:\frac{{{x^3}}}{{yz}} = \frac{x}{{{z^2}}}.\frac{{xz}}{{{y^3}}}.\frac{{yz}}{{{x^3}}} = \frac{{x.xz.yz}}{{{z^2}.{y^3}.{x^3}}} = \frac{{{x^2}y{z^2}}}{{{x^3}{y^3}{z^2}}} = \frac{1}{{x{y^2}}}\end{array}\)
Phân thức là một biểu thức đại số quan trọng trong toán học, và việc nắm vững các phép toán với phân thức là nền tảng cho việc học các kiến thức nâng cao hơn. Bài viết này sẽ trình bày chi tiết lý thuyết về nhân, chia phân thức theo chương trình SGK Toán 8 - Chân trời sáng tạo.
Trước khi đi vào các phép toán, chúng ta cần ôn lại khái niệm về phân thức. Một phân thức là một biểu thức có dạng A/B, trong đó A là tử thức và B là mẫu thức. Phân thức chỉ có nghĩa khi mẫu thức khác 0 (B ≠ 0).
Để nhân hai phân thức A/B và C/D, ta thực hiện như sau:
Công thức tổng quát: (A/B) * (C/D) = (A*C) / (B*D)
Để chia hai phân thức A/B cho C/D, ta thực hiện như sau:
Công thức tổng quát: (A/B) : (C/D) = (A/B) * (D/C) = (A*D) / (B*C)
Quy tắc đổi dấu phân thức rất quan trọng trong việc thực hiện các phép toán với phân thức. Quy tắc như sau:
Nói cách khác, nếu ta đổi dấu tử thức thì phải đổi dấu mẫu thức, và ngược lại.
Trước khi thực hiện các phép toán nhân, chia phân thức, ta nên rút gọn phân thức nếu có thể. Việc rút gọn phân thức giúp cho việc tính toán trở nên dễ dàng hơn và tránh được các sai sót.
Để rút gọn phân thức, ta tìm ước chung lớn nhất (ƯCLN) của tử thức và mẫu thức, sau đó chia cả tử thức và mẫu thức cho ƯCLN đó.
Ví dụ 1: Tính (2x/3y) * (5y/4x)
Giải:
(2x/3y) * (5y/4x) = (2x * 5y) / (3y * 4x) = 10xy / 12xy = 5/6
Ví dụ 2: Tính (x^2 + 1)/2 : (x + 1)/4
Giải:
(x^2 + 1)/2 : (x + 1)/4 = (x^2 + 1)/2 * 4/(x + 1) = (x^2 + 1) * 4 / (2 * (x + 1)) = (x^2 + 1) * 2 / (x + 1) = (2x^2 + 2) / (x + 1)
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về lý thuyết nhân, chia phân thức SGK Toán 8 - Chân trời sáng tạo. Chúc bạn học tập tốt!