Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 2 trang 20 SGK Toán 8 tập 1 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, rõ ràng và dễ tiếp thu nhất.
a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên
Video hướng dẫn giải
Thực hiện các phép nhân:
a) \(\left( {4 - x} \right)\left( {4 + x} \right)\)
b) \(\left( {2y + 7z} \right)\left( {2y - 7z} \right)\)
c) \(\left( {x + 2{y^2}} \right)\left( {x - 2{y^2}} \right)\)
Phương pháp giải:
Áp dụng hằng đẳng thức: Hiệu của hai bình phương.
Lời giải chi tiết:
a) \(\left( {4 - x} \right)\left( {4 + x} \right) = {4^2} - {x^2} = 16 - {x^2}\)
b) \(\left( {2y + 7z} \right)\left( {2y - 7z} \right) = {\left( {2y} \right)^2} - {\left( {7z} \right)^2} = 4{y^4} - 49{z^2}\)
c) \(\left( {x + 2{y^2}} \right)\left( {x - 2{y^2}} \right) = {x^2} - {\left( {2{y^2}} \right)^2} = {x^2} - 4{y^4}\)
Video hướng dẫn giải
Tính nhanh:
a) \(82.78\)
b) \(87.93\)
c) \({125^2} - {25^2}\)
Phương pháp giải:
Đưa tích của hai thừa số về dạng tích của một tổng và một hiệu rồi áp dụng hằng đẳng thức: Hiệu của hai bình phương.
Lời giải chi tiết:
a) \(82.78 = \left( {80 + 2} \right)\left( {80 - 2} \right) = {80^2} - {2^2} = 6400 - 4 = 6396\)
b) \(87.93 = \left( {90 - 3} \right)\left( {90 + 3} \right) = {90^2} - {3^2} = 8100 - 9 = 8091\)
c) \({125^2} - {25^2} = \left( {125 + 25} \right)\left( {125 - 25} \right) = 150.100 = 15000\)
Video hướng dẫn giải
a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.

b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức \(\left( {a + b} \right)\left( {a - b} \right)\) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?
Phương pháp giải:
a) Áp dụng công thức tính diện tích hình vuông
b) Áp dụng công thức tính diện tích hình chữ nhật, quy tắc nhân đa thức.
Lời giải chi tiết:
a) Diện tích Hình 3a là: \({a^2} - {b^2}\)
Diện tích Hình 3b là: \(\left( {a + b} \right)\left( {a - b} \right)\)
b) Ta có: \(\left( {a + b} \right)\left( {a - b} \right) = a.a - ab + ba - {b^2} = {a^2} - ab + ab - {b^2} = {a^2} - {b^2}\)
Suy ra: \(\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}\)
Vậy diện tích của hai hình bằng nhau.
Video hướng dẫn giải
Giải đáp câu hỏi ở đầu bài (trang 18)

Phương pháp giải:
Áp dụng hằng đẳng thức: Hiệu của hai bình phương
Lời giải chi tiết:
Ta có:
\({65^2} - {35^2} = \left( {65 + 35} \right)\left( {65 - 35} \right) = 100.30 = 3000\)
\(102.98 = \left( {100 + 2} \right)\left( {100 - 2} \right) = {100^2} - {2^2} = 10000 - 4 = 9996\)
Video hướng dẫn giải
a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.
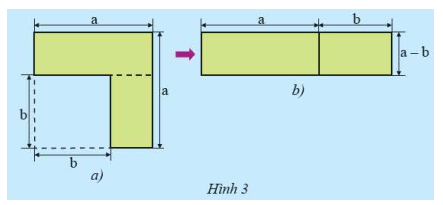
b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức \(\left( {a + b} \right)\left( {a - b} \right)\) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?
Phương pháp giải:
a) Áp dụng công thức tính diện tích hình vuông
b) Áp dụng công thức tính diện tích hình chữ nhật, quy tắc nhân đa thức.
Lời giải chi tiết:
a) Diện tích Hình 3a là: \({a^2} - {b^2}\)
Diện tích Hình 3b là: \(\left( {a + b} \right)\left( {a - b} \right)\)
b) Ta có: \(\left( {a + b} \right)\left( {a - b} \right) = a.a - ab + ba - {b^2} = {a^2} - ab + ab - {b^2} = {a^2} - {b^2}\)
Suy ra: \(\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}\)
Vậy diện tích của hai hình bằng nhau.
Video hướng dẫn giải
Thực hiện các phép nhân:
a) \(\left( {4 - x} \right)\left( {4 + x} \right)\)
b) \(\left( {2y + 7z} \right)\left( {2y - 7z} \right)\)
c) \(\left( {x + 2{y^2}} \right)\left( {x - 2{y^2}} \right)\)
Phương pháp giải:
Áp dụng hằng đẳng thức: Hiệu của hai bình phương.
Lời giải chi tiết:
a) \(\left( {4 - x} \right)\left( {4 + x} \right) = {4^2} - {x^2} = 16 - {x^2}\)
b) \(\left( {2y + 7z} \right)\left( {2y - 7z} \right) = {\left( {2y} \right)^2} - {\left( {7z} \right)^2} = 4{y^4} - 49{z^2}\)
c) \(\left( {x + 2{y^2}} \right)\left( {x - 2{y^2}} \right) = {x^2} - {\left( {2{y^2}} \right)^2} = {x^2} - 4{y^4}\)
Video hướng dẫn giải
Tính nhanh:
a) \(82.78\)
b) \(87.93\)
c) \({125^2} - {25^2}\)
Phương pháp giải:
Đưa tích của hai thừa số về dạng tích của một tổng và một hiệu rồi áp dụng hằng đẳng thức: Hiệu của hai bình phương.
Lời giải chi tiết:
a) \(82.78 = \left( {80 + 2} \right)\left( {80 - 2} \right) = {80^2} - {2^2} = 6400 - 4 = 6396\)
b) \(87.93 = \left( {90 - 3} \right)\left( {90 + 3} \right) = {90^2} - {3^2} = 8100 - 9 = 8091\)
c) \({125^2} - {25^2} = \left( {125 + 25} \right)\left( {125 - 25} \right) = 150.100 = 15000\)
Video hướng dẫn giải
Giải đáp câu hỏi ở đầu bài (trang 18)

Phương pháp giải:
Áp dụng hằng đẳng thức: Hiệu của hai bình phương
Lời giải chi tiết:
Ta có:
\({65^2} - {35^2} = \left( {65 + 35} \right)\left( {65 - 35} \right) = 100.30 = 3000\)
\(102.98 = \left( {100 + 2} \right)\left( {100 - 2} \right) = {100^2} - {2^2} = 10000 - 4 = 9996\)
Mục 2 trang 20 SGK Toán 8 tập 1 – Chân trời sáng tạo thường tập trung vào các bài tập về các phép toán với đa thức, bao gồm cộng, trừ, nhân, chia đa thức. Việc nắm vững các quy tắc và kỹ năng này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 8.
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 2 trang 20, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia đa thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu ngoặc, quy tắc đổi dấu và các phép toán với đa thức.
Bài tập này yêu cầu học sinh giải các phương trình bậc nhất một ẩn. Để giải bài tập này, học sinh cần nắm vững các quy tắc về chuyển vế, quy tắc nhân chia hai vế và các phép toán với số.
Bài tập này yêu cầu học sinh phân tích các đa thức thành nhân tử. Để giải bài tập này, học sinh cần nắm vững các phương pháp phân tích đa thức thành nhân tử, như đặt nhân tử chung, sử dụng hằng đẳng thức và nhóm đa thức.
Khi giải các bài tập trong mục 2 trang 20 SGK Toán 8 tập 1 – Chân trời sáng tạo, học sinh cần lưu ý những điều sau:
Kiến thức về các phép toán với đa thức và phân tích đa thức thành nhân tử có ứng dụng rất lớn trong việc giải quyết các bài toán Toán học khác, như giải phương trình, giải bất phương trình và chứng minh các đẳng thức.
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 20 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc các em học tập tốt!