Định lí Pythagore là một trong những định lý quan trọng nhất trong hình học, được học từ chương trình Toán 8. Bài viết này sẽ cung cấp cho bạn một cách đầy đủ và dễ hiểu về lý thuyết Định lí Pythagore trong sách giáo khoa Toán 8 - Chân trời sáng tạo.
Chúng ta sẽ cùng nhau tìm hiểu về nội dung định lý, cách chứng minh, các ứng dụng thực tế và các bài tập minh họa để giúp bạn nắm vững kiến thức này.
Định lí Pythagore
Định lí Pythagore
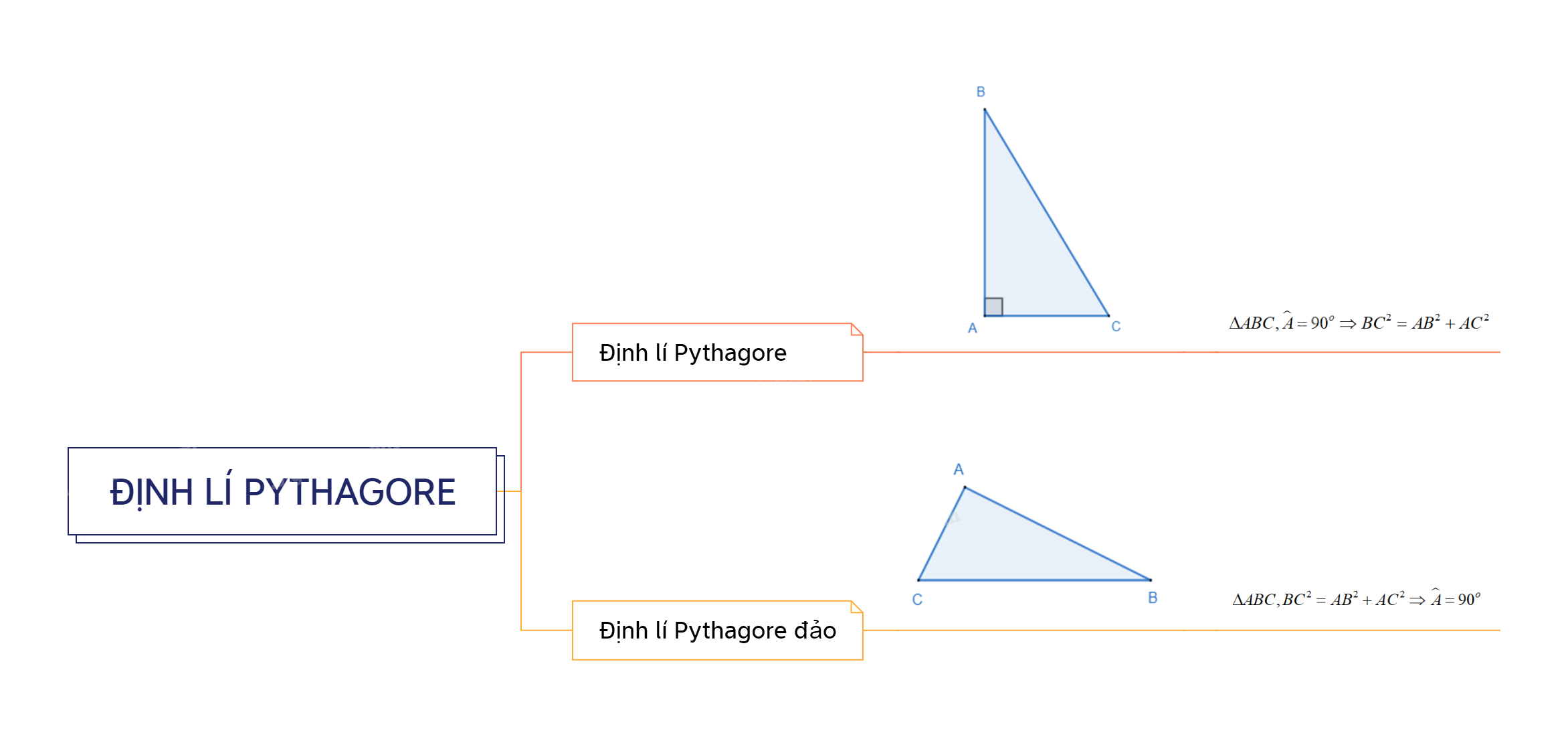
Trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.
\(\Delta ABC,\widehat A = {90^o} \Rightarrow B{C^2} = A{B^2} + A{C^2}\)
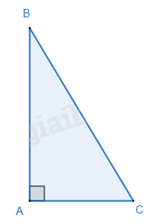
Định lí Pythagore đảo
Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.
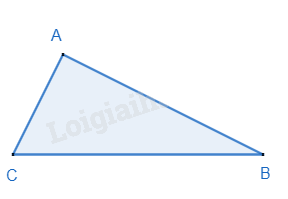
\(\Delta ABC,B{C^2} = A{B^2} + A{C^2} \Rightarrow \widehat A = {90^o}\)
Ví dụ:
Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do \({3^2} + {4^2} = {5^2}\), suy ra \[B{C^2} = A{B^2} + A{C^2}\].
Định lí Pythagore là nền tảng của hình học tam giác vuông, và việc hiểu rõ lý thuyết này là rất quan trọng cho việc giải quyết các bài toán liên quan. Bài viết này sẽ trình bày chi tiết lý thuyết Định lí Pythagore theo chương trình SGK Toán 8 - Chân trời sáng tạo, giúp học sinh nắm vững kiến thức một cách dễ dàng.
Trước khi đi vào Định lí Pythagore, chúng ta cần hiểu rõ về tam giác vuông. Tam giác vuông là tam giác có một góc vuông (90 độ). Trong một tam giác vuông:
Định lí Pythagore phát biểu rằng: Trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông.
Công thức: a2 + b2 = c2
Trong đó:
Có nhiều cách chứng minh Định lí Pythagore. Một trong những cách chứng minh phổ biến nhất là sử dụng diện tích hình vuông:
(Phần này sẽ mô tả chi tiết cách chứng minh bằng hình vẽ và giải thích, có thể sử dụng các thẻ HTML như div, span để trình bày hình ảnh và chú thích)
Định lí Pythagore có rất nhiều ứng dụng trong thực tế và trong các lĩnh vực khác của toán học:
Dưới đây là một số bài tập vận dụng Định lí Pythagore:
(Phần này sẽ cung cấp lời giải chi tiết cho từng bài tập)
Ngoài các bài tập tính độ dài cạnh, Định lí Pythagore còn xuất hiện trong nhiều dạng bài tập khác nhau, như:
Khi sử dụng Định lí Pythagore, cần lưu ý:
Định lí Pythagore là một phần quan trọng của hình học Euclid. Ngoài ra, còn có các định lý liên quan đến tam giác vuông, như định lý cosin, định lý sin. Việc tìm hiểu thêm về các định lý này sẽ giúp bạn có cái nhìn toàn diện hơn về hình học.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Định lí Pythagore SGK Toán 8 - Chân trời sáng tạo. Chúc bạn học tập tốt!