Chào mừng bạn đến với bài học về Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm trong chương trình SGK Toán 8 - Chân trời sáng tạo tại giaitoan.edu.vn. Xác suất là một lĩnh vực toán học quan trọng, giúp chúng ta dự đoán khả năng xảy ra của các sự kiện trong cuộc sống.
Bài học này sẽ cung cấp cho bạn kiến thức cơ bản về xác suất, bao gồm khái niệm, công thức và các ứng dụng thực tế. Chúng tôi sẽ đi sâu vào cả lý thuyết và thực hành để đảm bảo bạn hiểu rõ và có thể áp dụng kiến thức này vào giải các bài tập.
Xác suất lí thuyết là gì?
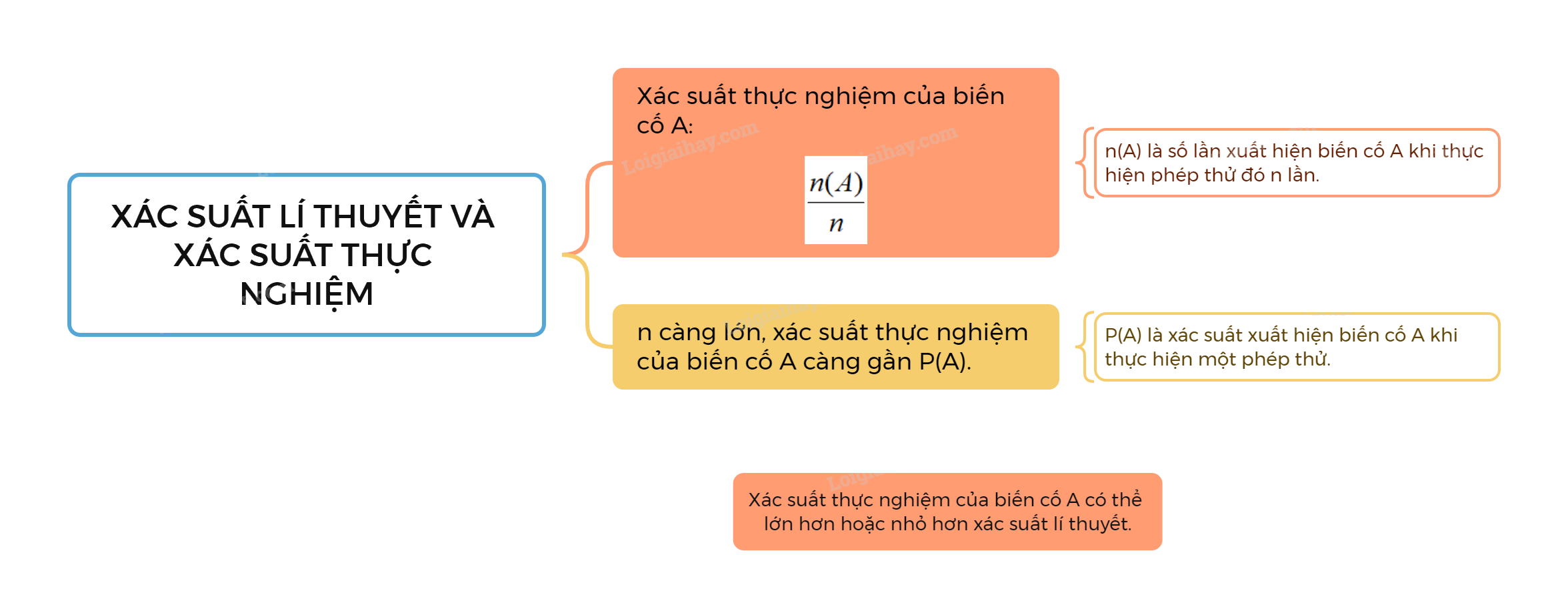
Gọi P(A) là xác suất xuất hiện biến cố A khi thực hiện một phép thử.
Gọi n(A) là số lần xuất hiện biến cố A khi thực hiện phép thử đó n lần.
Xác suất thực nghiệm của biến cố A là tỉ số \(\frac{{n(A)}}{n}\).
Khi n càng lớn, xác suất thực nghiệm của biến cố A càng gần P(A).
Nhận xét:
Xác suất thực nghiệm của biến cố A có thể lớn hơn hoặc nhỏ hơn xác suất lí thuyết.
Xác suất là một khái niệm toán học quan trọng, được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống. Trong chương trình Toán 8, học sinh bắt đầu làm quen với những kiến thức cơ bản về xác suất, bao gồm lý thuyết xác suất và xác suất thực nghiệm. Bài viết này sẽ cung cấp một cái nhìn tổng quan về hai khái niệm này, cùng với các ví dụ minh họa và bài tập thực hành.
Lý thuyết xác suất nghiên cứu các hiện tượng ngẫu nhiên, tức là các hiện tượng mà kết quả không thể dự đoán trước một cách chắc chắn. Trong lý thuyết xác suất, chúng ta quan tâm đến việc tính toán khả năng xảy ra của một sự kiện nào đó.
Các khái niệm cơ bản:
Công thức tính xác suất:
P(A) = (Số kết quả thuận lợi cho A) / (Tổng số kết quả có thể xảy ra)
Xác suất thực nghiệm là xác suất được tính dựa trên kết quả của một số lượng lớn các phép thử thực tế. Thay vì dựa trên lý thuyết, xác suất thực nghiệm dựa trên quan sát và thống kê.
Cách tính xác suất thực nghiệm:
Xác suất thực nghiệm của biến cố A = (Số lần biến cố A xảy ra) / (Tổng số lần thực hiện phép thử)
| Đặc điểm | Lý thuyết Xác suất | Xác suất Thực nghiệm |
|---|---|---|
| Nguồn gốc | Dựa trên lý thuyết và suy luận logic | Dựa trên kết quả của các phép thử thực tế |
| Tính chính xác | Chính xác nếu không gian mẫu là hữu hạn và các kết quả là đồng khả năng | Càng chính xác khi số lượng phép thử càng lớn |
| Ứng dụng | Dự đoán khả năng xảy ra của các sự kiện trong các tình huống lý tưởng | Đánh giá khả năng xảy ra của các sự kiện trong thực tế |
Ví dụ 1: Tung một đồng xu 100 lần, kết quả được 55 lần mặt Sấp và 45 lần mặt Ngửa. Tính xác suất thực nghiệm của biến cố “tung đồng xu được mặt Sấp”.
Giải:
Xác suất thực nghiệm của biến cố “tung đồng xu được mặt Sấp” = 55 / 100 = 0.55
Ví dụ 2: Một hộp có 10 quả bóng, trong đó có 3 quả bóng màu đỏ, 4 quả bóng màu xanh và 3 quả bóng màu vàng. Lấy ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất của biến cố “lấy được quả bóng màu đỏ”.
Giải:
Tổng số quả bóng trong hộp là 10.
Số quả bóng màu đỏ là 3.
Xác suất của biến cố “lấy được quả bóng màu đỏ” = 3 / 10 = 0.3
| Mặt xúc xắc | Số lần xuất hiện |
|---|---|
| 1 | 7 |
| 2 | 9 |
| 3 | 11 |
| 4 | 8 |
| 5 | 10 |
| 6 | 5 |
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm trong chương trình Toán 8 - Chân trời sáng tạo. Chúc bạn học tập tốt!