Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 66 SGK Toán 8 tập 2 – Chân trời sáng tạo. Bài học này thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
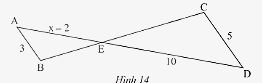
Trong Hình 14, cho biết
Đề bài
Trong Hình 14, cho biết \(AB//CD\)
a) Chứng minh rằng \(\Delta AEB\backsim\Delta DEC\).
b) Tìm \(x\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng cắt phần kéo dài của hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết
a) Xét tam giác \(ABE\) có:
\(AB//CD\) và \(C,D\) cắt \(BE;AE\) lần lượt tại \(C,D\).
Do đó, \(\Delta AEB\backsim\Delta DEC\) (định lí)
b) Vì \(\Delta AEB\backsim\Delta DEC\) nên \(\frac{{AE}}{{ED}} = \frac{{AB}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Thay số ta được:
\(\frac{{x - 2}}{{10}} = \frac{3}{5} \Rightarrow x - 2 = \frac{{10.3}}{5} = 6 \Rightarrow x = 6 + 2 = 8\)
Vậy \(x = 8\).
Bài 4 trang 66 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về hình bình hành, hình chữ nhật, hình thoi và hình vuông để giải quyết các bài toán liên quan đến tính chất đường chéo, diện tích và các yếu tố khác của các hình này. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Để giúp các em hiểu rõ hơn về cách giải bài 4 trang 66 SGK Toán 8 tập 2 – Chân trời sáng tạo, chúng ta sẽ đi vào phân tích từng phần của bài toán. Bài toán thường yêu cầu chứng minh một tính chất nào đó của hình hoặc tính toán các yếu tố như độ dài đường chéo, diện tích, chu vi,…
Bước đầu tiên trong quá trình giải bài toán là đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh sai sót trong quá trình giải.
Việc vẽ hình minh họa giúp chúng ta hình dung rõ hơn về bài toán và dễ dàng tìm ra mối liên hệ giữa các yếu tố. Sau khi vẽ hình, chúng ta đánh dấu các yếu tố đã biết trong đề bài để làm cơ sở cho việc giải toán.
Dựa trên các kiến thức đã học và hình vẽ minh họa, chúng ta vận dụng các phương pháp giải phù hợp để giải quyết bài toán. Các phương pháp thường được sử dụng bao gồm:
Sau khi giải xong bài toán, chúng ta cần kiểm tra lại kết quả để đảm bảo tính chính xác. Sau đó, trình bày lời giải một cách rõ ràng, logic và dễ hiểu.
Đề bài: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng AF = 2FC.
Lời giải:
Để củng cố kiến thức và kỹ năng giải bài toán về hình học, các em có thể luyện tập thêm các bài toán tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi giải các bài toán khó.
Bài 4 trang 66 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài toán quan trọng giúp các em hiểu rõ hơn về các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ giải quyết bài toán này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!