Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 63, 64, 65 sách giáo khoa Toán 8 tập 2 – Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
a) Nếu
Video hướng dẫn giải
a) Nếu \(\Delta A'B'C' = \Delta ABC\)thì tam giác \(A'B'C'\) có đồng dạng với tam giác \(ABC\) không? Tỉ số đồng dạng là bao nhiêu?
b) Cho tam giác \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng \(k\) thì \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số nào?
Phương pháp giải:
Hai tam giác bằng nhau thì các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Tỉ số đồng dạng là tỉ số các cạnh tương ứng.
Lời giải chi tiết:
a) Nếu \(\Delta A'B'C' = \Delta ABC\)thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\)theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\)đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).
Video hướng dẫn giải
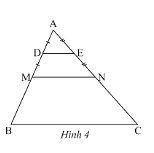
Quan sát Hình 4, cho biết \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,DE\)là đường trung bình của tam giác \(AMN,MN\) là đường trung bình của tam giác \(ABC.\) Tam giác \(ADE\) đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng là bao nhiêu?
Phương pháp giải:
Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu
\(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\end{array} \right.\)
Tỉ số đồng dạng là \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\)
Lời giải chi tiết:
Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)
Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)
Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)
\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)
Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\)nên \(\Delta ADE\backsim\Delta ABC\)
Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).
Vậy tỉ số đồng dạng là \(\frac{1}{4}\).
Video hướng dẫn giải
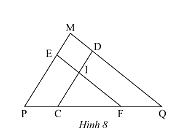
Quan sát Hình 8, cho biết \(DC//MP,EF//MQ\).
a) Chứng minh rằng \(\Delta EPF\backsim\Delta DCQ\).
b) \(\Delta ICF\) có đồng dạng với \(\Delta MPQ\)không? Tại sao?
Phương pháp giải:
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) và \(\Delta ABC\backsim\Delta A''B''C''\) thì \(\Delta A'B'C'\backsim\Delta A''B''C''\).
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết:
a) Xét tam giác \(MPQ\)có \(EF//MQ\) nên \(\Delta MPQ\backsim\Delta EPF\) (định lí) (1)
Xét tam giác \(MPQ\)có \(DC//MP\) nên \(\Delta MPQ\backsim\Delta DCQ\) (định lí) (2)
Từ (1) và (2) \(\Delta EPF\backsim\Delta DCQ\) (tính chất tam giác đồng dạng)
b) Xét tam giác \(EPF\)có \(IC//EP\) nên \(\Delta ICF\backsim\Delta EPF\) (định lí) (3)
Từ (1) và (3) suy ra, \(\Delta ICF\backsim\Delta MPQ\).
Video hướng dẫn giải
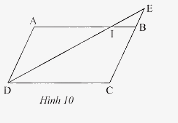
Trong Hình 10, cho biết \(ABCD\) là hình bình hành.
a) Chứng minh rằng \(\Delta IEB\backsim\Delta IDA\).
b) Cho biết \(CB = 3BE\) và \(AI = 9cm\). Tính \(DC\).
Phương pháp giải:
Nếu một đường thẳng cắt phần kéo dài của hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết:
a) Do \(ABCD\) là hình bình hành nên \(BC//AD \Rightarrow EB//AD\)
Xét tam giác \(IDA\) có
\(EB//AD;EB\) cắt \(AI;ID\) tại \(B;E\).
Do đó, \(\Delta IEB\backsim\Delta IDA\) (định lí)
b) Ta có: \(\Delta IEB\backsim\Delta IDA \Rightarrow \frac{{IB}}{{IA}} = \frac{{BE}}{{DA}}\) (hai cặp cạnh tương ứng tỉ lệ).
Mà \(CB = AD;CB = 3BE \Rightarrow AD = 3BE;AI = 9cm\) nên ta có:
\(\frac{{IB}}{9} = \frac{{BE}}{{3BE}} = \frac{1}{3} \Rightarrow IB = \frac{{9.1}}{3} = 3(cm)\).
\(\Rightarrow AB = AI + IB = 9 + 3 = 12cm\)Mà DC = AB (ABCD là hình bình hành \(\Rightarrow DC = 12cm\)
Vậy \(DC = 12cm.\)
Video hướng dẫn giải
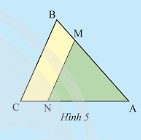
Quan sát Hình 5, biết \(MN//BC\). Hãy điển ? cho thích hợp.
\(\Delta AMN\) và\(\Delta ABC\) có:
\(\widehat A\) chung;
\(\widehat M = ?\);
\(\widehat N = ?\);
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{?}{?}\)
Nêu nhận xét về mối quan hệ giữa tam giác \(AMN\) và tam giác \(ABC\).
Phương pháp giải:
- Tính chất hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì sẽ tạo ra các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
- Hệ quả định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Vì \(MN//BC\) nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\) (các cặp góc đồng vị)
Xét tam giác \(ABC\) có, \(MN//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Vậy trong các ô trống cần điền là:
\(\widehat A\) chung;
\(\widehat M = \widehat B\);
\(\widehat N = \widehat C\);
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Tam giác \(\Delta AMN\) và\(\Delta ABC\) có các góc tương ứng bằng nhau và tỉ số các cạnh tương ứng bằng nhau nên \(\Delta AMN\) đồng dạng \(\Delta ABC\).
Video hướng dẫn giải
a) Nếu \(\Delta A'B'C' = \Delta ABC\)thì tam giác \(A'B'C'\) có đồng dạng với tam giác \(ABC\) không? Tỉ số đồng dạng là bao nhiêu?
b) Cho tam giác \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng \(k\) thì \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số nào?
Phương pháp giải:
Hai tam giác bằng nhau thì các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Tỉ số đồng dạng là tỉ số các cạnh tương ứng.
Lời giải chi tiết:
a) Nếu \(\Delta A'B'C' = \Delta ABC\)thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\)theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\)đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).
Video hướng dẫn giải
Quan sát Hình 4, cho biết \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,DE\)là đường trung bình của tam giác \(AMN,MN\) là đường trung bình của tam giác \(ABC.\) Tam giác \(ADE\) đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng là bao nhiêu?
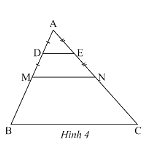
Phương pháp giải:
Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu
\(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\end{array} \right.\)
Tỉ số đồng dạng là \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\)
Lời giải chi tiết:
Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)
Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)
Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)
\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)
Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\)nên \(\Delta ADE\backsim\Delta ABC\)
Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).
Vậy tỉ số đồng dạng là \(\frac{1}{4}\).
Video hướng dẫn giải
Quan sát Hình 5, biết \(MN//BC\). Hãy điển ? cho thích hợp.
\(\Delta AMN\) và\(\Delta ABC\) có:
\(\widehat A\) chung;
\(\widehat M = ?\);
\(\widehat N = ?\);
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{?}{?}\)
Nêu nhận xét về mối quan hệ giữa tam giác \(AMN\) và tam giác \(ABC\).
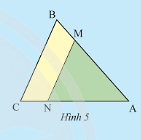
Phương pháp giải:
- Tính chất hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì sẽ tạo ra các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
- Hệ quả định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Vì \(MN//BC\) nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\) (các cặp góc đồng vị)
Xét tam giác \(ABC\) có, \(MN//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Vậy trong các ô trống cần điền là:
\(\widehat A\) chung;
\(\widehat M = \widehat B\);
\(\widehat N = \widehat C\);
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Tam giác \(\Delta AMN\) và\(\Delta ABC\) có các góc tương ứng bằng nhau và tỉ số các cạnh tương ứng bằng nhau nên \(\Delta AMN\) đồng dạng \(\Delta ABC\).
Video hướng dẫn giải
Quan sát Hình 8, cho biết \(DC//MP,EF//MQ\).
a) Chứng minh rằng \(\Delta EPF\backsim\Delta DCQ\).
b) \(\Delta ICF\) có đồng dạng với \(\Delta MPQ\)không? Tại sao?
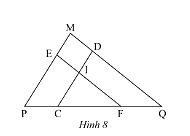
Phương pháp giải:
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) và \(\Delta ABC\backsim\Delta A''B''C''\) thì \(\Delta A'B'C'\backsim\Delta A''B''C''\).
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết:
a) Xét tam giác \(MPQ\)có \(EF//MQ\) nên \(\Delta MPQ\backsim\Delta EPF\) (định lí) (1)
Xét tam giác \(MPQ\)có \(DC//MP\) nên \(\Delta MPQ\backsim\Delta DCQ\) (định lí) (2)
Từ (1) và (2) \(\Delta EPF\backsim\Delta DCQ\) (tính chất tam giác đồng dạng)
b) Xét tam giác \(EPF\)có \(IC//EP\) nên \(\Delta ICF\backsim\Delta EPF\) (định lí) (3)
Từ (1) và (3) suy ra, \(\Delta ICF\backsim\Delta MPQ\).
Video hướng dẫn giải
Trong Hình 10, cho biết \(ABCD\) là hình bình hành.
a) Chứng minh rằng \(\Delta IEB\backsim\Delta IDA\).
b) Cho biết \(CB = 3BE\) và \(AI = 9cm\). Tính \(DC\).
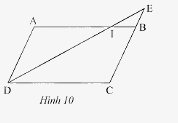
Phương pháp giải:
Nếu một đường thẳng cắt phần kéo dài của hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết:
a) Do \(ABCD\) là hình bình hành nên \(BC//AD \Rightarrow EB//AD\)
Xét tam giác \(IDA\) có
\(EB//AD;EB\) cắt \(AI;ID\) tại \(B;E\).
Do đó, \(\Delta IEB\backsim\Delta IDA\) (định lí)
b) Ta có: \(\Delta IEB\backsim\Delta IDA \Rightarrow \frac{{IB}}{{IA}} = \frac{{BE}}{{DA}}\) (hai cặp cạnh tương ứng tỉ lệ).
Mà \(CB = AD;CB = 3BE \Rightarrow AD = 3BE;AI = 9cm\) nên ta có:
\(\frac{{IB}}{9} = \frac{{BE}}{{3BE}} = \frac{1}{3} \Rightarrow IB = \frac{{9.1}}{3} = 3(cm)\).
\(\Rightarrow AB = AI + IB = 9 + 3 = 12cm\)Mà DC = AB (ABCD là hình bình hành \(\Rightarrow DC = 12cm\)
Vậy \(DC = 12cm.\)
Mục 2 của chương trình Toán 8 tập 2 – Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về hình học, đặc biệt là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Các bài tập trong mục này yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng suy luận.
Bài tập này yêu cầu học sinh nhắc lại các định nghĩa, tính chất của hình bình hành, cách chứng minh một tứ giác là hình bình hành. Các em cần nắm vững các dấu hiệu nhận biết hình bình hành để áp dụng vào giải bài tập.
Bài tập này tập trung vào việc ôn tập các tính chất của hình chữ nhật, mối quan hệ giữa đường chéo và các cạnh của hình chữ nhật. Học sinh cần hiểu rõ các định lý liên quan đến hình chữ nhật để giải quyết các bài toán về tính độ dài cạnh, đường chéo, diện tích và chu vi của hình chữ nhật.
Bài tập này yêu cầu học sinh ôn tập các tính chất của hình thoi, mối quan hệ giữa đường chéo và các cạnh của hình thoi. Các em cần nắm vững các định lý liên quan đến hình thoi để giải quyết các bài toán về tính độ dài cạnh, đường chéo, diện tích và chu vi của hình thoi.
Bài tập này tập trung vào việc ôn tập các tính chất của hình vuông, mối quan hệ giữa đường chéo và các cạnh của hình vuông. Học sinh cần hiểu rõ các định lý liên quan đến hình vuông để giải quyết các bài toán về tính độ dài cạnh, đường chéo, diện tích và chu vi của hình vuông.
Bài tập: Cho hình bình hành ABCD, có góc A bằng 60 độ. Tính các góc còn lại của hình bình hành.
Giải:
Để nắm vững kiến thức và rèn luyện kỹ năng giải toán, các em nên làm thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với các mức độ khó khác nhau để các em có thể lựa chọn.
Học toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Hãy dành thời gian ôn tập lý thuyết, làm bài tập và tìm hiểu các phương pháp giải toán hiệu quả. Chúc các em học tốt!
| Hình | Tính chất |
|---|---|
| Hình bình hành | Các cạnh đối song song và bằng nhau, các góc đối bằng nhau, đường chéo cắt nhau tại trung điểm của mỗi đường. |
| Hình chữ nhật | Có bốn góc vuông, các cạnh đối song song và bằng nhau, đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường. |
| Hình thoi | Có bốn cạnh bằng nhau, các cạnh đối song song, đường chéo cắt nhau vuông góc tại trung điểm của mỗi đường. |
| Hình vuông | Có bốn cạnh bằng nhau và bốn góc vuông, đường chéo bằng nhau, cắt nhau vuông góc tại trung điểm của mỗi đường. |