Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 1 Chân trời sáng tạo của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong sách giáo khoa, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 1 trang 49, 50 tập trung vào các kiến thức cơ bản về đa thức, các phép toán trên đa thức và ứng dụng của chúng. Bài viết này sẽ hướng dẫn các em từng bước giải các bài tập, đồng thời cung cấp các ví dụ minh họa để các em hiểu rõ hơn về lý thuyết.
Nam làm một chiếc hộp hình chóp tứ giác đều như Hình 1a
Video hướng dẫn giải
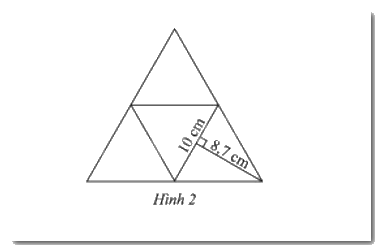
Một tấm bìa (Hình 2) gấp thành hình chóp tam giác đều với các mặt đều là hình tam giác đều. Với số đo trên hình vẽ, hãy tính diện tích xung quanh và diện tích toàn phần của hình này.
Phương pháp giải:
Sử dụng công thức tính diện tích xung quanh và diện tích toàn phẩn của hình chóp tam giác đều.
Lời giải chi tiết:
Diện tích một mặt của hình chóp là: \(10.8,7:2 = 43,5\) (\(c{m^2}\))
Diện tích xung quanh của hình chóp là: \(43,5.3 = 130,5\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là: \(43,5.4 = 174\) (\(c{m^2}\))
Video hướng dẫn giải
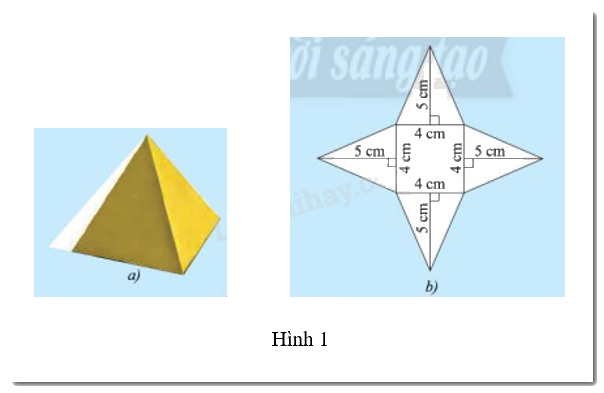
Nam làm một chiếc hộp hình chóp tứ giác đều như Hình 1a, sau đó Nam trải các mặt của chiếc hộp với các số đo đã cho như Hình 1b. Hãy cho biết:
a) Hình này có bao nhiêu mặt bên
b) Diện tích của mỗi mặt bên
c) Diện tích của tất cả các mặt bên
d) Diện tích đáy của hình này
Phương pháp giải:
Sử dụng công thức tính diện tích các mặt bên (tam giác), đáy (hình vuông)
Lời giải chi tiết:
a) Hình này có 4 mặt bên
b) Diện tích của mỗi mặt bên là: \(4.5:2 = 10\) (\(c{m^2}\))
c) Diện tích của tất cả các mặt bên là: \(10.4 = 40\) (\(c{m^2}\))
d) Diện tích đáy là: \(4.4 = 16\) (\(c{m^2}\))
Video hướng dẫn giải
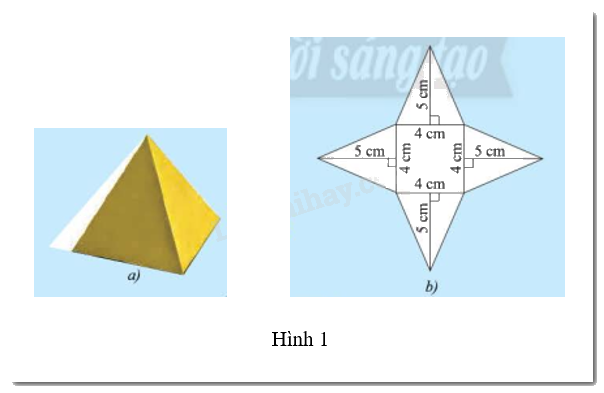
Nam làm một chiếc hộp hình chóp tứ giác đều như Hình 1a, sau đó Nam trải các mặt của chiếc hộp với các số đo đã cho như Hình 1b. Hãy cho biết:
a) Hình này có bao nhiêu mặt bên
b) Diện tích của mỗi mặt bên
c) Diện tích của tất cả các mặt bên
d) Diện tích đáy của hình này
Phương pháp giải:
Sử dụng công thức tính diện tích các mặt bên (tam giác), đáy (hình vuông)
Lời giải chi tiết:
a) Hình này có 4 mặt bên
b) Diện tích của mỗi mặt bên là: \(4.5:2 = 10\) (\(c{m^2}\))
c) Diện tích của tất cả các mặt bên là: \(10.4 = 40\) (\(c{m^2}\))
d) Diện tích đáy là: \(4.4 = 16\) (\(c{m^2}\))
Video hướng dẫn giải
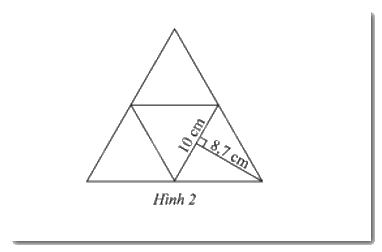
Một tấm bìa (Hình 2) gấp thành hình chóp tam giác đều với các mặt đều là hình tam giác đều. Với số đo trên hình vẽ, hãy tính diện tích xung quanh và diện tích toàn phần của hình này.
Phương pháp giải:
Sử dụng công thức tính diện tích xung quanh và diện tích toàn phẩn của hình chóp tam giác đều.
Lời giải chi tiết:
Diện tích một mặt của hình chóp là: \(10.8,7:2 = 43,5\) (\(c{m^2}\))
Diện tích xung quanh của hình chóp là: \(43,5.3 = 130,5\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là: \(43,5.4 = 174\) (\(c{m^2}\))
Mục 1 của chương trình Toán 8 tập 1 Chân trời sáng tạo giới thiệu về các khái niệm cơ bản của đa thức, bao gồm định nghĩa, các loại đa thức (đơn thức, đa thức nhiều biến), và các phép toán trên đa thức (cộng, trừ, nhân, chia). Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Đa thức là biểu thức đại số gồm một hoặc nhiều đơn thức được cộng lại với nhau. Đơn thức là biểu thức đại số chỉ chứa các biến và các hệ số. Ví dụ, 3x2y là một đơn thức, còn 2x2y + 5x - 1 là một đa thức.
Để thực hiện các phép toán trên đa thức, ta cần tuân theo các quy tắc sau:
Bài tập yêu cầu thu gọn các đa thức sau: a) 3x2 + 2x - 5x2 + 7x; b) 4xy - 2x2 + 3xy + x2.
Giải:
Bài tập yêu cầu tìm bậc của các đa thức sau: a) 5x3 - 2x2 + 1; b) -3xy2 + 4x2y - 2.
Giải:
Bài tập yêu cầu thực hiện các phép tính sau: a) (2x + 3y) + (x - y); b) (5x2 - 2x + 1) - (3x2 + x - 4).
Giải:
Đa thức có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để học tốt về đa thức, các em cần:
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về mục 1 trang 49, 50 Sách giáo khoa Toán 8 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt!