Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 2 trang 8 sách giáo khoa Toán 8 tập 1, chương trình Chân trời sáng tạo.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Để tính thể tích của hình hộp chữ nhật ở hình 2, bạn An viết (V = 3xy.2x), còn bạn Tâm viết (V = 6{x^2}y). Nêu nhận xét về kết quả của hai bạn
Video hướng dẫn giải
Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng.
a) \(12x{y^2}x\)
b) \( - y\left( {2z} \right)y\)
c) \({x^3}yx\)
d) \(5{x^2}{y^3}{z^4}y\)
Phương pháp giải:
- Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến chỉ xuất hiện một lần dưới dạng nâng lên lũy thừa với số mũ nguyên dương.
- Số nói trên gọi là hệ số
- Tổng số mũ của tất cả các biến có trong đơn thức (có hệ số khác \(0\)) gọi là bậc của đơn thức đó.
Lời giải chi tiết:
a) Ta có: \(12x{y^2}x = 12.\left( {x.x} \right).{y^2} = 12{x^2}{y^2}\)
Đơn thức trên có hệ số là \(12\), bậc bằng \(2 + 2 = 4\).
b) Ta có: \( - y\left( {2z} \right)y = - 2.\left( {y.y} \right).z = - 2{y^2}z\)
Đơn thức trên có hệ số là \( - 2\), bậc bằng \(2 + 1 = 3\).
c) Ta có: \({x^3}yx = \left( {{x^3}.x} \right).y = {x^4}y\)
Đơn thức trên có hệ số là \(1\), bậc bằng \(4 + 1 = 5\).
d) Ta có: \(5{x^2}{y^3}{z^4}y = 5{x^2}.\left( {{y^3}.y} \right).{z^4} = 5{x^2}{y^4}{z^4}\)
Đơn thức trên có hệ số là \(5\), bậc bằng \(2 + 4 + 4 = 10\).
Video hướng dẫn giải
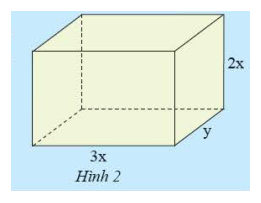
Để tính thể tích của hình hộp chữ nhật ở hình 2, bạn An viết \(V = 3xy.2x\), còn bạn Tâm viết \(V = 6{x^2}y\). Nêu nhận xét về kết quả của hai bạn.
Phương pháp giải:
Thu gọn các đơn thức.
Lời giải chi tiết:
Ta có: \(V = 3xy.2x = \left( {3.2} \right).\left( {x.x} \right).y = 6{x^2}y\)
Kết quả của hai bạn An và Tâm là giống nhau.
Video hướng dẫn giải
Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng.
a) \(12x{y^2}x\)
b) \( - y\left( {2z} \right)y\)
c) \({x^3}yx\)
d) \(5{x^2}{y^3}{z^4}y\)
Phương pháp giải:
- Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến chỉ xuất hiện một lần dưới dạng nâng lên lũy thừa với số mũ nguyên dương.
- Số nói trên gọi là hệ số
- Tổng số mũ của tất cả các biến có trong đơn thức (có hệ số khác \(0\)) gọi là bậc của đơn thức đó.
Lời giải chi tiết:
a) Ta có: \(12x{y^2}x = 12.\left( {x.x} \right).{y^2} = 12{x^2}{y^2}\)
Đơn thức trên có hệ số là \(12\), bậc bằng \(2 + 2 = 4\).
b) Ta có: \( - y\left( {2z} \right)y = - 2.\left( {y.y} \right).z = - 2{y^2}z\)
Đơn thức trên có hệ số là \( - 2\), bậc bằng \(2 + 1 = 3\).
c) Ta có: \({x^3}yx = \left( {{x^3}.x} \right).y = {x^4}y\)
Đơn thức trên có hệ số là \(1\), bậc bằng \(4 + 1 = 5\).
d) Ta có: \(5{x^2}{y^3}{z^4}y = 5{x^2}.\left( {{y^3}.y} \right).{z^4} = 5{x^2}{y^4}{z^4}\)
Đơn thức trên có hệ số là \(5\), bậc bằng \(2 + 4 + 4 = 10\).
Video hướng dẫn giải
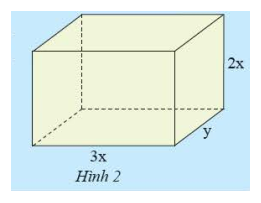
Để tính thể tích của hình hộp chữ nhật ở hình 2, bạn An viết \(V = 3xy.2x\), còn bạn Tâm viết \(V = 6{x^2}y\). Nêu nhận xét về kết quả của hai bạn.
Phương pháp giải:
Thu gọn các đơn thức.
Lời giải chi tiết:
Ta có: \(V = 3xy.2x = \left( {3.2} \right).\left( {x.x} \right).y = 6{x^2}y\)
Kết quả của hai bạn An và Tâm là giống nhau.
Mục 2 trang 8 SGK Toán 8 tập 1 – Chân trời sáng tạo thường tập trung vào các bài tập vận dụng kiến thức về các phép toán cơ bản, các tính chất của số thực, và các biểu thức đại số đơn giản. Việc nắm vững kiến thức nền tảng là yếu tố then chốt để giải quyết thành công các bài tập trong mục này.
Để giúp bạn hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 8, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh tính giá trị của một biểu thức đại số cho trước. Để giải bài tập này, bạn cần:
Ví dụ: Tính giá trị của biểu thức 2x + 3y khi x = 1 và y = 2.
Giải:
2x + 3y = 2 * 1 + 3 * 2 = 2 + 6 = 8
Bài tập này yêu cầu học sinh rút gọn một biểu thức đại số phức tạp. Để giải bài tập này, bạn cần:
Ví dụ: Rút gọn biểu thức (x + 2)^2 - 4x.
Giải:
(x + 2)^2 - 4x = x^2 + 4x + 4 - 4x = x^2 + 4
Bài tập này yêu cầu học sinh giải một phương trình đơn giản. Để giải bài tập này, bạn cần:
Ví dụ: Giải phương trình 3x - 6 = 0.
Giải:
3x - 6 = 0 => 3x = 6 => x = 2
Để giải các bài tập trong mục 2 trang 8 SGK Toán 8 tập 1 – Chân trời sáng tạo một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Kiến thức về các phép toán cơ bản, các tính chất của số thực, và các biểu thức đại số có ứng dụng rất lớn trong thực tế. Ví dụ, bạn có thể sử dụng kiến thức này để tính toán chi phí mua hàng, tính lãi suất ngân hàng, hoặc giải quyết các bài toán liên quan đến vật lý, hóa học, sinh học.
Hy vọng rằng với những hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả trên đây, bạn sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 8 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc bạn học tập tốt!
| Bài tập | Mức độ khó | Lời khuyên |
|---|---|---|
| Bài 1 | Dễ | Chú ý thứ tự thực hiện các phép toán. |
| Bài 2 | Trung bình | Sử dụng các hằng đẳng thức đại số. |
| Bài 3 | Dễ | Chuyển phương trình về dạng ax + b = 0. |